题目内容
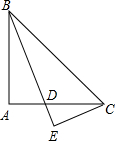 已知:△ABC是等腰直角三角形,∠A=90°,BD平分∠ABC交AC于点D,CE⊥BD.
已知:△ABC是等腰直角三角形,∠A=90°,BD平分∠ABC交AC于点D,CE⊥BD.求证:BD=2CE.
考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:延长BA和CE交于点M,首先证明△BME≌△BCE可得EM=EC=
MC,再证明△ABD≌△ACM可得DB=MC,利用等量代换可得BD=2CE.
| 1 |
| 2 |
解答: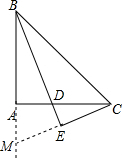 证明:延长BA和CE交于点M,
证明:延长BA和CE交于点M,
∵CE⊥BD,
∴∠BEC=∠BEM=90°,
∵BD平分∠ABC,
∴∠MBE=∠CBE,
在△BME和△BCE中
,
∴△BME≌△BCE(ASA),
∴EM=EC=
MC,
∵△ABC是等腰直角三角形,
∴∠BAC=∠MAC=90°,BA=AC,
∴∠ABD+∠BDA=90°,
∵∠BEC=90°,
∴∠ACM+∠CBE=90°,
∵∠BDA=∠EDC,
∴∠ABE=∠ACM,
在△ABD和△ACM中
,
∴△ABD≌△ACM(ASA),
∴DB=MC,
∴BD=2CE.
 证明:延长BA和CE交于点M,
证明:延长BA和CE交于点M,∵CE⊥BD,
∴∠BEC=∠BEM=90°,
∵BD平分∠ABC,
∴∠MBE=∠CBE,
在△BME和△BCE中
|
∴△BME≌△BCE(ASA),
∴EM=EC=
| 1 |
| 2 |
∵△ABC是等腰直角三角形,
∴∠BAC=∠MAC=90°,BA=AC,
∴∠ABD+∠BDA=90°,
∵∠BEC=90°,
∴∠ACM+∠CBE=90°,
∵∠BDA=∠EDC,
∴∠ABE=∠ACM,
在△ABD和△ACM中
|
∴△ABD≌△ACM(ASA),
∴DB=MC,
∴BD=2CE.
点评:此题主要考查了全等三角形的判定和性质,以及等腰直角三角形的性质,关键是正确证明EM=EC=
MC和DB=MC.
| 1 |
| 2 |

练习册系列答案
相关题目
 如图,拦水坝的横断面为梯形ABCD,根据图中的数据求:
如图,拦水坝的横断面为梯形ABCD,根据图中的数据求: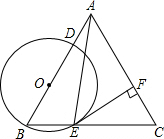 如图,在△ABC中,AB=AC,tanC=3,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F,且BD=2EF.
如图,在△ABC中,AB=AC,tanC=3,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F,且BD=2EF. 一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线成45°角,水流最高点B比喷头A高2米.
一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线成45°角,水流最高点B比喷头A高2米. 已知:如图,△ABC和△ADE都是等边三角形.求证:∠ACD=∠ABE.
已知:如图,△ABC和△ADE都是等边三角形.求证:∠ACD=∠ABE.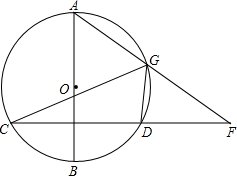 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,G是
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,G是
 如图,△ABC的三个顶点坐标分别为A(-4,-2),B(-5,-4),C(0,-4),作一个平移,平面内任意一点P(x0,y0)的像是点P′(x0+7,y0+6),△ABC的像是△A′B′C′,求△A′B′C′的三个顶点A′,B′,C′的坐标.
如图,△ABC的三个顶点坐标分别为A(-4,-2),B(-5,-4),C(0,-4),作一个平移,平面内任意一点P(x0,y0)的像是点P′(x0+7,y0+6),△ABC的像是△A′B′C′,求△A′B′C′的三个顶点A′,B′,C′的坐标.