题目内容
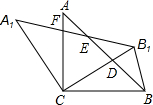 如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设CB1交AB于D,A1B1分别交AB,AC于E,F
如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设CB1交AB于D,A1B1分别交AB,AC于E,F(1)求证:△CBD≌△CA1F;
(2)试用含α的代数式表示∠B1BD;
(3)当α等于多少度时,△BB1D是等腰三角形.
考点:全等三角形的判定与性质
专题:
分析:(1)根据已知条件,利用旋转的性质及全等三角形的判定方法,来判定三角形全等.
(2)利用等腰直角三角形的性质得到∠CBA=45°.然后由旋转的性质推知BC=B1C,则∠CB1B=∠CBB1,所以根据三角形内角和定理进行解答即可.
(3)当△BBD是等腰三角形时,要分别讨论B1B=B1D、BB1=BD、B1D=DB三种情况,第一,三种情况不成立,只有第二种情况成立,求得α=30°.
(2)利用等腰直角三角形的性质得到∠CBA=45°.然后由旋转的性质推知BC=B1C,则∠CB1B=∠CBB1,所以根据三角形内角和定理进行解答即可.
(3)当△BBD是等腰三角形时,要分别讨论B1B=B1D、BB1=BD、B1D=DB三种情况,第一,三种情况不成立,只有第二种情况成立,求得α=30°.
解答: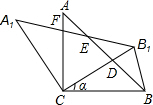 (1)证明:∵AC=BC,
(1)证明:∵AC=BC,
∴∠A=∠ABC.
∵△ABC绕点C逆时针旋转角α(0°<α<90°)得到△A1B1C,
∴∠A1=∠A,A1C=AC,∠ACA1=∠BCB1=α.
∴∠A1=∠CBD,A1C=BC.
在△CBD与△CA1F中,
,
∴△CBD≌△CA1F(ASA).
(2)∵在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°.
又由旋转的性质得到BC=B1C,则∠CB1B=∠CBB1,
∴∠CB1B=∠CBB1=
=90°-
.
∴∠B1BD=∠CBB1-∠CBA=90°-
-45°=45°-
;
(3)在△CBB1中,∵CB=CB1
∴∠CBB1=∠CB1B=
(180°-α).
又∵△ABC是等腰直角三角形,
∴∠ABC=45°.
①若B1B=B1D,则∠B1DB=∠B1BD,
∵∠B1DB=45°+α,∠B1BD=∠CBB1-45°=
(180°-α)-45°=45°-
,
∴45°+α=45°-
,
∴α=0°(舍去);
②∵∠BB1C=∠B1BC>∠B1BD,
∴BD>B1D,即BD≠B1D;
③若BB1=BD,则∠BDB1=∠BB1D,即45°+α=
(180°-α),α=30°
由①②③可知,当△BB1D为等腰三角形时,α=30°.
 (1)证明:∵AC=BC,
(1)证明:∵AC=BC,∴∠A=∠ABC.
∵△ABC绕点C逆时针旋转角α(0°<α<90°)得到△A1B1C,
∴∠A1=∠A,A1C=AC,∠ACA1=∠BCB1=α.
∴∠A1=∠CBD,A1C=BC.
在△CBD与△CA1F中,
|
∴△CBD≌△CA1F(ASA).
(2)∵在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°.
又由旋转的性质得到BC=B1C,则∠CB1B=∠CBB1,
∴∠CB1B=∠CBB1=
| 180°-α |
| 2 |
| α |
| 2 |
∴∠B1BD=∠CBB1-∠CBA=90°-
| α |
| 2 |
| α |
| 2 |
(3)在△CBB1中,∵CB=CB1
∴∠CBB1=∠CB1B=
| 1 |
| 2 |
又∵△ABC是等腰直角三角形,
∴∠ABC=45°.
①若B1B=B1D,则∠B1DB=∠B1BD,
∵∠B1DB=45°+α,∠B1BD=∠CBB1-45°=
| 1 |
| 2 |
| α |
| 2 |
∴45°+α=45°-
| α |
| 2 |
∴α=0°(舍去);
②∵∠BB1C=∠B1BC>∠B1BD,
∴BD>B1D,即BD≠B1D;
③若BB1=BD,则∠BDB1=∠BB1D,即45°+α=
| 1 |
| 2 |
由①②③可知,当△BB1D为等腰三角形时,α=30°.
点评:本题考查三角形全等的判定与性质,判定两个三角形全等的一般方法有:SSS、SAS、SAA、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
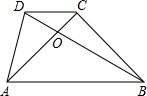 在四边形ABCD中,AB∥CD,对角线AC、BD交于点O,3CD=2AB,则S△ADC:S△AOB=( )
在四边形ABCD中,AB∥CD,对角线AC、BD交于点O,3CD=2AB,则S△ADC:S△AOB=( )| A、4:9 | B、6:9 |
| C、8:9 | D、10:9 |
若一个正多边形的一个外角为60°,则它的内切圆半径与外接圆半径之比是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
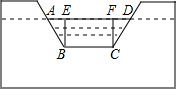 如图,利用土埂修筑一条渠道,在埂中间挖去深为0.6m的一块(图中的阴影部分),其横截面是梯形ABCD,其中,AB=CD,已知渠道内坡度为1:1.5,渠道地面宽BC为0.5m.
如图,利用土埂修筑一条渠道,在埂中间挖去深为0.6m的一块(图中的阴影部分),其横截面是梯形ABCD,其中,AB=CD,已知渠道内坡度为1:1.5,渠道地面宽BC为0.5m.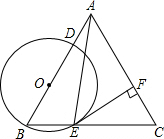 如图,在△ABC中,AB=AC,tanC=3,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F,且BD=2EF.
如图,在△ABC中,AB=AC,tanC=3,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F,且BD=2EF. 一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线成45°角,水流最高点B比喷头A高2米.
一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线成45°角,水流最高点B比喷头A高2米. 已知:如图,△ABC和△ADE都是等边三角形.求证:∠ACD=∠ABE.
已知:如图,△ABC和△ADE都是等边三角形.求证:∠ACD=∠ABE.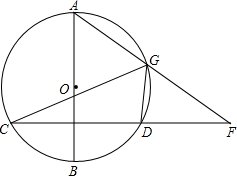 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,G是
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,G是