题目内容
已知P为⊙O内一点，OP=2，如果⊙O的半径是3，那么过P点的最短弦长是（ ）
| A、1 | ||
| B、2 | ||
C、
| ||
D、2
|
考点：垂径定理,勾股定理
专题：计算题
分析：过点P作弦AB⊥OP，此时AB为过P点的最短弦，如图，根据垂径定理得AP=BP，然后在Rt△APO中利用勾股定理计算出AP=
，则AB=2AP=2
．
| 5 |
| 5 |
解答：解：
过点P作弦AB⊥OP，此时AB为过P点的最短弦，如图，
∵OP⊥AB，
∴AP=BP，
在Rt△APO中，∵OP=2，OA=3，
∴AP=
=
，
∴AB=2AP=2
．
故选D．
过点P作弦AB⊥OP，此时AB为过P点的最短弦，如图，∵OP⊥AB，
∴AP=BP，
在Rt△APO中，∵OP=2，OA=3，
∴AP=
| OA2-OP2 |
| 5 |
∴AB=2AP=2
| 5 |
故选D．
点评：本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理．
练习册系列答案
活力课时同步练习册系列答案
学业测评一课一测系列答案
相关题目
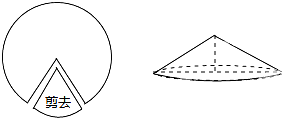
如图，如果从半径为5cm的圆形纸片上剪去
圆周的一个扇形，将留下的扇形围成一个圆锥（接缝处不重叠），则这个圆锥的高为（ ）
| 1 |
| 5 |
| A、1cm | ||
| B、3cm | ||
C、2
| ||
| D、4cm |
如图，线段AB是⊙O的直径，弦CD⊥AB，∠CAB=20°，则∠AOD等于根据图中数字的规律，最后一个空格应填的数是（ ）
| A、738 | B、720 |
| C、550 | D、500 |
如图，两直线AB，CD相交于点O，已知OE平分∠BOD，且∠AOC：∠AOD=3：7，
小聪和小明沿同一条路同时从学校出发到市图书馆查阅资料，小聪骑电动车，小明骑自行车，当小聪从原路回到学校时，小明刚好到市图书馆，图中折线O-A-B-C和线段OD分别表示两人离学校的路程s（千米）与所经过的时间t（小时）之间的函数关系，请根据图象回答下列问题：