题目内容
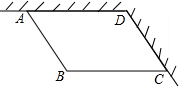 某小区准备修建一个平行四边形花坛,花坛的一组邻边利用足够长的成120°角的两面墙,另两条边利用长度和为40米的篱笆.围成的花坛是如图所示的平行四边形ABCD,其中∠ADC=120°,设AB边长为x米,平行四边形ABCD的面积为S平方米.
某小区准备修建一个平行四边形花坛,花坛的一组邻边利用足够长的成120°角的两面墙,另两条边利用长度和为40米的篱笆.围成的花坛是如图所示的平行四边形ABCD,其中∠ADC=120°,设AB边长为x米,平行四边形ABCD的面积为S平方米.(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)根据小区的规划要求,所修建花坛的面积是150
| 3 |
考点:一元二次方程的应用,根据实际问题列二次函数关系式
专题:
分析:(1)作BH⊥AD于点H,设AB=x,根据平行四边形的性质就可以得出BH=
x,BC=40-x,由平行四边形的面积公式就可以得出结论;
(2)当S=150
代入(1)的解析式求出结论即可.
| ||
| 2 |
(2)当S=150
| 3 |
解答:解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠DAB=180°-∠ADC=60°.
作BH⊥AD于点H,
∵AB=x,
∴BH=x•sin60°=
x,BC=40-x,
∴S=
x(40-x)=-
x2+20
x.
∴S与x之间的函数关系式为:S=-
x2+20
x;
(2)由题意,得
150
=-
x2+20
x,
解得:
x1=10,x2=30
∴AB边长10米,BC边长30米.
∴AB∥CD,

∴∠DAB=180°-∠ADC=60°.
作BH⊥AD于点H,
∵AB=x,
∴BH=x•sin60°=
| ||
| 2 |
∴S=
| ||
| 2 |
| ||
| 2 |
| 3 |
∴S与x之间的函数关系式为:S=-
| ||
| 2 |
| 3 |
(2)由题意,得
150
| 3 |
| ||
| 2 |
| 3 |
解得:
x1=10,x2=30
∴AB边长10米,BC边长30米.
点评:本题考查了三角函数值的运用,平行四边形的面积公式的运用,一元二次方程的解法的运用,解答时由平行四边形的面积公式建立函数关系式是关键.

练习册系列答案
相关题目
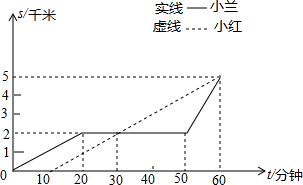 小红与小兰从学校出发到距学校5千米的书店买书,下图反应了他们两人离开学校的路程与时间的关系.根据图形尝解决你们提出的问题.
小红与小兰从学校出发到距学校5千米的书店买书,下图反应了他们两人离开学校的路程与时间的关系.根据图形尝解决你们提出的问题. 如图,已知∠1+∠2=180°,∠DAE=∠BCF.
如图,已知∠1+∠2=180°,∠DAE=∠BCF.