题目内容
 如图,已知∠1+∠2=180°,∠DAE=∠BCF.
如图,已知∠1+∠2=180°,∠DAE=∠BCF.(1)试判断直线AE与CF有怎样的位置关系?并说明理由;
(2)若∠BCF=70°,求∠ADF的度数;
(3)若DA平分∠BDF,请说明BC平分∠DBE.
考点:平行线的判定与性质
专题:计算题
分析:(1)AE与CF平行,理由为:由邻补角定义及已知两角互补,等量代换得到一对同位角相等,利用同位角相等两直线平行即可得证;
(2)由AE与CF平行,得到一对同旁内角互补,根据∠DAE=∠BCF,等量代换得到另一对同旁内角互补,利用同旁内角互补两直线平行得到AB与CD平行,利用两直线平行同位角相等即可求出所求角的度数;
(3)由DA为角平分线得到一对角相等,再利用两直线平行同位角相等、内错角相等,等量代换得到∠DBC=∠CBE,即可得证.
(2)由AE与CF平行,得到一对同旁内角互补,根据∠DAE=∠BCF,等量代换得到另一对同旁内角互补,利用同旁内角互补两直线平行得到AB与CD平行,利用两直线平行同位角相等即可求出所求角的度数;
(3)由DA为角平分线得到一对角相等,再利用两直线平行同位角相等、内错角相等,等量代换得到∠DBC=∠CBE,即可得证.
解答:解:(1)AE∥CF,理由为:
∵∠2+∠BDC=180°,∠2+∠1=180°,
∴∠1=∠BDC,
∴AE∥CF;
(2)∵AE∥CF,
∴∠ABC+∠BCF=180°,
∵∠DAE=∠BCF,
∴∠ABC+∠DAE=180°,
∴AD∥BC,
∴∠ADF=∠BCF=70°;
(3)∵DA平分∠BDF,
∴∠ADF=∠ADB,
∵AD∥BC,AE∥CF,
∴∠ADF=∠C=∠EBC,∠ADB=∠CBD,
∴∠ABD=∠CBD,
则BC平分∠DBE.
∵∠2+∠BDC=180°,∠2+∠1=180°,
∴∠1=∠BDC,
∴AE∥CF;
(2)∵AE∥CF,
∴∠ABC+∠BCF=180°,
∵∠DAE=∠BCF,
∴∠ABC+∠DAE=180°,
∴AD∥BC,
∴∠ADF=∠BCF=70°;
(3)∵DA平分∠BDF,
∴∠ADF=∠ADB,
∵AD∥BC,AE∥CF,
∴∠ADF=∠C=∠EBC,∠ADB=∠CBD,
∴∠ABD=∠CBD,
则BC平分∠DBE.
点评:此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
相关题目
 一个汽车车牌在水中的倒影如图,则该车的牌照号码是
一个汽车车牌在水中的倒影如图,则该车的牌照号码是

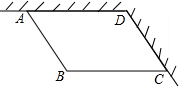 某小区准备修建一个平行四边形花坛,花坛的一组邻边利用足够长的成120°角的两面墙,另两条边利用长度和为40米的篱笆.围成的花坛是如图所示的平行四边形ABCD,其中∠ADC=120°,设AB边长为x米,平行四边形ABCD的面积为S平方米.
某小区准备修建一个平行四边形花坛,花坛的一组邻边利用足够长的成120°角的两面墙,另两条边利用长度和为40米的篱笆.围成的花坛是如图所示的平行四边形ABCD,其中∠ADC=120°,设AB边长为x米,平行四边形ABCD的面积为S平方米.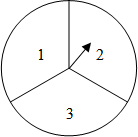 如图,一个可以自由转动的转盘被等分成3个扇形区域,上面分别标有数字1、2、3.甲、乙两位同学用该转盘做游戏.
如图,一个可以自由转动的转盘被等分成3个扇形区域,上面分别标有数字1、2、3.甲、乙两位同学用该转盘做游戏.