题目内容
20.矩形各个内角的平分线围成一个四边形,则这个四边形一定是( )| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 平行四边形 |
分析 由矩形的性质和角平分线证出四边形GMON为矩形,再证出△DOC、△AMD、△BNC是等腰直角三角形,得出OD=OC,证明△AMD≌△BNC,得出NC=DM,得出OM=ON,即可得出结论.
解答 解:如图所示:∵四边形ABCD是矩形,
∴∠BAD=∠CBA=∠BCD=∠ADC=90°, AD=BC,
AD=BC,
∵AF,BE是矩形的内角平分线.
∴∠DAM=∠BAF=∠ABE=∠CBE=45°.
∴∠1=∠2=90°.
同理:∠MON=∠OMG=90°,
∴四边形GMON为矩形.
又∵AF、BE、DK、CJ为矩形ABCD的角的平分线,
∴△DOC、△AMD、△BNC是等腰直角三角形,
∴OD=OC,
在△AMD和△BNC中,
$\left\{\begin{array}{l}{∠AMD=∠BNC}&{\;}\\{∠DAM=∠CBN}&{\;}\\{AD=BC}&{\;}\end{array}\right.$,
∴△AMD≌△BNC(AAS),
∴NC=DM,
∴NC-OC=DM-OD,
即OM=ON,
∴矩形GMON为正方形.
故选:A.
点评 本题考查了矩形的性质与判定、正方形的判定、等腰直角三角形的判定与性质、全等三角形的判定与性质;熟练掌握矩形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
8. 如图,AB=AC,BE平分∠ABC,DE∥BC,图中等腰三角形共有( )
如图,AB=AC,BE平分∠ABC,DE∥BC,图中等腰三角形共有( )
 如图,AB=AC,BE平分∠ABC,DE∥BC,图中等腰三角形共有( )
如图,AB=AC,BE平分∠ABC,DE∥BC,图中等腰三角形共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.要调查某校九年级550名学生周日的睡眠时间,下列调查对象选取最合适的是( )
| A. | 选取该校一个班级的学生 | B. | 随机选取该校50名九年级学生 | ||
| C. | 选取该校50名九年级女生 | D. | 选取该校50名男生 |
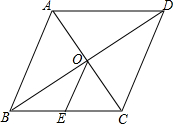 如图,菱形ABCD的对角线AC、BD交于点O,AC=6cm,BD=8cm,点E是边BC的中点,连接OE,则OE=2.5cm.
如图,菱形ABCD的对角线AC、BD交于点O,AC=6cm,BD=8cm,点E是边BC的中点,连接OE,则OE=2.5cm.