题目内容
12.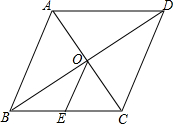 如图,菱形ABCD的对角线AC、BD交于点O,AC=6cm,BD=8cm,点E是边BC的中点,连接OE,则OE=2.5cm.
如图,菱形ABCD的对角线AC、BD交于点O,AC=6cm,BD=8cm,点E是边BC的中点,连接OE,则OE=2.5cm.
分析 根据菱形的对角线互相垂直平分求出OB,OC,AC⊥BD,再利用勾股定理列式求出BC,然后根据三角形的中位线平行于第三边并且等于第三边的一半求解即可.
解答 解:∵菱形ABCD的对角线AC、BD相交于点O,
∴OB=$\frac{1}{2}$BD=$\frac{1}{2}$×8=4cm,OA=OC=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3cm,AC⊥BD,
由勾股定理得,BC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
又∵点E为BC中点,
∴OE是△ABC的中位线,
∴OE=$\frac{1}{2}$AB=$\frac{1}{2}$×5=2.5cm.
故答案为:2.5cm.
点评 本题考查了菱形的性质,三角形的中位线平行于第三边并且等于第三边的一半,勾股定理,熟记性质与定理是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
2.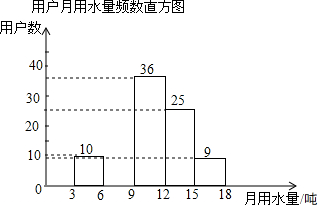 水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m=20,n=0.25;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
 水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:| 用户月用水量频数分布表 | ||
| 平均用水量(吨) | 频数 | 频率 |
| 3~6吨 | 10 | 0.1 |
| 6~9吨 | m | 0.2 |
| 9~12吨 | 36 | 0.36 |
| 12~15吨 | 25 | n |
| 15~18吨 | 9 | 0.09 |
(1)在频数分布表中:m=20,n=0.25;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
20.矩形各个内角的平分线围成一个四边形,则这个四边形一定是( )
| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 平行四边形 |
17.计算($\frac{1}{4}$)-2的结果等于( )
| A. | -$\frac{1}{8}$ | B. | $\frac{1}{8}$ | C. | -16 | D. | 16 |
4.下列各式从左到右的变形为分解因式的是( )
| A. | m2-m-6=(m+2)(m-3) | B. | (m+2)(m-3)=m2-m-6 | ||
| C. | x2+8x-9=(x+3)(m-3)+8x | D. | 18x3y2=3x3y2•6 |
1.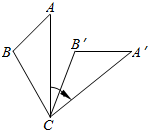 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是( )
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是( )
 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是( )
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是( )| A. | 90° | B. | 80° | C. | 50° | D. | 30° |