题目内容
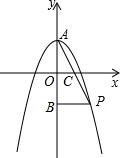 如图,抛物线y=ax2+2与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,若AC=PC,且S△AOC=1,记点A关于x轴的对称点为B.连结BP.
如图,抛物线y=ax2+2与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,若AC=PC,且S△AOC=1,记点A关于x轴的对称点为B.连结BP.(1)求BP的长;
(2)求抛物线与x轴的交点坐标.
考点:抛物线与x轴的交点,三角形中位线定理
专题:
分析:(1)根据三角形的面积公式求得OC的长度;然后利用点A与点B关于x轴对称求得OA=OB=2,则根据三角形中位线的性质求得BP=2OC;
(2)由(1)得出P点坐标,再利用待定系数法求出a的值,进而得出图象与x轴交点坐标.
(2)由(1)得出P点坐标,再利用待定系数法求出a的值,进而得出图象与x轴交点坐标.
解答:解:(1)当x=0时,y=2,则OA=2.
∵S△AOC=
OC•OA=1,
∴OC=1.
∵A关于x轴的对称点为B,
∴OA=OB=2,
∵AC=PC,
∴OC为△APB的中位线,
∴BP=2OC=2;
(2)∵OC为△APB的中位线,OA⊥OC,
∴PB⊥y轴,
∴点P的坐标为(2,-2),
∵点P(2,-2)在函数y=ax2+2的图象上,
∴a=-1,
∴y=-x2+2.
当y=0时,-x2+2=0,
∴x1=
,x2=-
,
∴抛物线与x轴的交点坐标是(
,0),(-
,0 ).
∵S△AOC=
| 1 |
| 2 |
∴OC=1.
∵A关于x轴的对称点为B,
∴OA=OB=2,
∵AC=PC,
∴OC为△APB的中位线,
∴BP=2OC=2;
(2)∵OC为△APB的中位线,OA⊥OC,
∴PB⊥y轴,
∴点P的坐标为(2,-2),
∵点P(2,-2)在函数y=ax2+2的图象上,
∴a=-1,
∴y=-x2+2.
当y=0时,-x2+2=0,
∴x1=
| 2 |
| 2 |
∴抛物线与x轴的交点坐标是(
| 2 |
| 2 |
点评:此题主要考查了抛物线与x轴交点求法以及相似三角形的判定与性质等知识,得出P点坐标是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,M是四边形ABCD对角线的交点,AC⊥x轴于点C,BD⊥y轴于点B.反比例函数C1:y=
如图,M是四边形ABCD对角线的交点,AC⊥x轴于点C,BD⊥y轴于点B.反比例函数C1:y=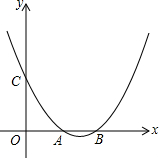 已知二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A、B,若点A的坐标是(1,0),点B在点A的右侧.
已知二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A、B,若点A的坐标是(1,0),点B在点A的右侧.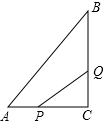 在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从点C出发沿CB边向点B以2cm/s的速度移动.
在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从点C出发沿CB边向点B以2cm/s的速度移动.