题目内容
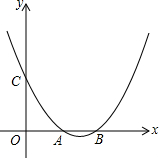 已知二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A、B,若点A的坐标是(1,0),点B在点A的右侧.
已知二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A、B,若点A的坐标是(1,0),点B在点A的右侧.(1)c=
(2)求a的取值范围;
(3)若过点C且平行于x轴的直线交该抛物线于另一点D,AD、BC交于点P,记△PCD的面积为S1,△PAB的面积为S2,求S1-S2的值.
考点:二次函数综合题
专题:
分析:(1)将点C(0,1)代入二次函数y=ax2+bx+c(a>0),即可求得c的值;将点A(1,0),代入二次函数y=ax2+bx+c(a>0),即可用含a的代数式表示b;
(2)将点A(1,0)代入二次函数y=ax2+bx+1(a>0),可得a+b+1=0,即b=-(a+1),二次函数与x轴交于不同的两点,根据判别式可得a≠1,点B在点A的右侧,可得对称轴直线x=-
>1.从而得到a的取值范围是:0<a<1;
(3)解方程:ax2-(a+1)x+1=0,得AB=
.把y=1代入y=ax2-(a+1)x+1,得CD=
.S1-S2=S△PCD-S△PAB=S△ACD-S△CAB,根据三角形面积公式代入计算即可求解.
(2)将点A(1,0)代入二次函数y=ax2+bx+1(a>0),可得a+b+1=0,即b=-(a+1),二次函数与x轴交于不同的两点,根据判别式可得a≠1,点B在点A的右侧,可得对称轴直线x=-
| b |
| 2a |
(3)解方程:ax2-(a+1)x+1=0,得AB=
| 1-a |
| a |
| a+1 |
| a |
解答:解:(1)将点C(0,1)代入二次函数y=ax2+bx+c(a>0),可得1=0+0+c,
解得,c=1;
将点A(1,0),代入二次函数y=ax2+bx+c(a>0),可得a+b+1=0,
解得,b=-1-a;
故答案为:1;-1-a;
(2)将点A(1,0)代入二次函数y=ax2+bx+1(a>0),可得a+b+1=0,即b=-(a+1),
∵二次函数与x轴交于不同的两点,
∴△=b2-4ac=(a-1)2>0,
∴a≠1,
∵点B在点A的右侧,
∴对称轴直线x=-
>1.
∵a>0,
∴2a+b<0,
∴a<1,
∴a的取值范围是:0<a<1;
 (3)解方程:ax2-(a+1)x+1=0,
(3)解方程:ax2-(a+1)x+1=0,
得:x1=1,x2=
.
∴AB=
.
把y=1代入y=ax2-(a+1)x+1,得x1=0,x2=
.
∴CD=
.
∵S1-S2=S△PCD-S△PAB=S△ACD-S△CAB,
∴S1-S2=
×
×1-
×
×1=1.
故答案为:1.
解得,c=1;
将点A(1,0),代入二次函数y=ax2+bx+c(a>0),可得a+b+1=0,
解得,b=-1-a;
故答案为:1;-1-a;
(2)将点A(1,0)代入二次函数y=ax2+bx+1(a>0),可得a+b+1=0,即b=-(a+1),
∵二次函数与x轴交于不同的两点,
∴△=b2-4ac=(a-1)2>0,
∴a≠1,
∵点B在点A的右侧,
∴对称轴直线x=-
| b |
| 2a |
∵a>0,
∴2a+b<0,
∴a<1,
∴a的取值范围是:0<a<1;
 (3)解方程:ax2-(a+1)x+1=0,
(3)解方程:ax2-(a+1)x+1=0,得:x1=1,x2=
| 1 |
| a |
∴AB=
| 1-a |
| a |
把y=1代入y=ax2-(a+1)x+1,得x1=0,x2=
| a+1 |
| a |
∴CD=
| a+1 |
| a |
∵S1-S2=S△PCD-S△PAB=S△ACD-S△CAB,
∴S1-S2=
| 1 |
| 2 |
| a+1 |
| a |
| 1 |
| 2 |
| 1-a |
| a |
故答案为:1.
点评:考查了二次函数综合题,涉及的知识点有:代入法的运用,根与判别式的关系,对称轴公式,解方程,三角形面积计算,综合性较强.

练习册系列答案
相关题目
下列一元二次方程用配方法解比较简单的是( )
| A、x2-x-5=0 |
| B、(x-2)2=5 |
| C、x2+4x-6=0 |
| D、x2-3x=0 |
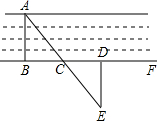 要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )
要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )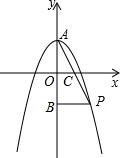 如图,抛物线y=ax2+2与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,若AC=PC,且S△AOC=1,记点A关于x轴的对称点为B.连结BP.
如图,抛物线y=ax2+2与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,若AC=PC,且S△AOC=1,记点A关于x轴的对称点为B.连结BP.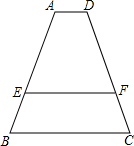 如图,已知AD∥EF∥BC,AD=2,BC=6,AE2=AB•EB,则EF=
如图,已知AD∥EF∥BC,AD=2,BC=6,AE2=AB•EB,则EF=