题目内容
 如图,M是四边形ABCD对角线的交点,AC⊥x轴于点C,BD⊥y轴于点B.反比例函数C1:y=
如图,M是四边形ABCD对角线的交点,AC⊥x轴于点C,BD⊥y轴于点B.反比例函数C1:y=| 4 |
| x |
(1)求经过点M的反比例函数图象的解析式;
(2)若点D恰好也在图象C1上,试证明四边形ABCD是菱形.
考点:反比例函数综合题
专题:
分析:(1)设出A坐标为(m,n),根据M为AC中点,且AC垂直与x轴,确定出M坐标,首先根据已知反比例函数经过点A求得mn的乘积,然后将点M的坐标代入设出的反比例函数的解析式求解即可;
(2)根据DB垂直于y轴,得到D与M纵坐标相同,将M纵坐标代入反比例解析式中求出x的值,确定出D坐标,得到BM=DM,进而确定出AC与BD互相平分,又AC与BD垂直,利用对角线互相平分且垂直的四边形为菱形即可得证.
(2)根据DB垂直于y轴,得到D与M纵坐标相同,将M纵坐标代入反比例解析式中求出x的值,确定出D坐标,得到BM=DM,进而确定出AC与BD互相平分,又AC与BD垂直,利用对角线互相平分且垂直的四边形为菱形即可得证.
解答:(1)解:设A(m,n),
∵M是AC的中点,AC⊥x轴于点C,
∴M(m,0.5n),
∵反比例函数C1:y=
的图象经过点A,
∴n=
,
∴mn=4,
设经过点M的反比例函数的解析式为y=
,
∴0.5n=
,
解得:k=0.5mn=0.5×4=2,
∴经过点M的反比例函数的解析式为y=
;
(2)证明:设A(m,n),则M(m,0.5n),
∵DB⊥y轴,
∴D与M纵坐标相同,
将y=0.5n代入y=
中,得x=2m,即D(2m,0.5n),
∴BM=DM=m,
∵M为AC中点,即AM=CM,
∴AC与BD互相平分,
∵AC⊥BD,
则四边形ABCD为菱形.
∵M是AC的中点,AC⊥x轴于点C,
∴M(m,0.5n),
∵反比例函数C1:y=
| 4 |
| x |
∴n=
| 4 |
| m |
∴mn=4,
设经过点M的反比例函数的解析式为y=
| k |
| x |
∴0.5n=
| k |
| m |
解得:k=0.5mn=0.5×4=2,
∴经过点M的反比例函数的解析式为y=
| 2 |
| x |
(2)证明:设A(m,n),则M(m,0.5n),
∵DB⊥y轴,
∴D与M纵坐标相同,
将y=0.5n代入y=
| 4 |
| x |
∴BM=DM=m,
∵M为AC中点,即AM=CM,
∴AC与BD互相平分,
∵AC⊥BD,
则四边形ABCD为菱形.
点评:此题属于反比例函数综合题,涉及的知识有:坐标与图形性质,反比例函数性质,以及菱形的判定,熟练掌握反比例函数的性质是解本题的关键.

练习册系列答案
相关题目
以2、4为两边长的三角形的第三边长是方程x2-7x+10=0的根,则这个三角形的周长为( )
| A、8 | B、11 |
| C、11或8 | D、以上都不对 |
下列一元二次方程用配方法解比较简单的是( )
| A、x2-x-5=0 |
| B、(x-2)2=5 |
| C、x2+4x-6=0 |
| D、x2-3x=0 |
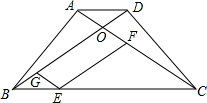 (1)如图,已知在梯形ABCD中AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G.
(1)如图,已知在梯形ABCD中AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G.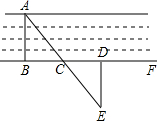 要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )
要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )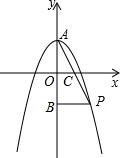 如图,抛物线y=ax2+2与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,若AC=PC,且S△AOC=1,记点A关于x轴的对称点为B.连结BP.
如图,抛物线y=ax2+2与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,若AC=PC,且S△AOC=1,记点A关于x轴的对称点为B.连结BP.