题目内容
设x1、x2是关于x的一元二次方程x2+x+n-2=mx的两个实数根,且x1<0,x2-3x1<0,求m、n的取值范围.
考点:一元二次方程根的分布
专题:
分析:根据x1<0,x2-3x1<0,判断出x2<0,然后根据根与系数的关系列出x1+x2=m-1,x1x2=n-2,求出m、n的取值范围即可.
解答:解:∵x2-3x1<0,
∴x2<3x1,
∵x1<0,
∴x2<0.
∵x1,x2是关于x的一元二次方程x2+x+n-2=mx(x2+(1-m)x+n-2=0)的两个实数根,
∴x1+x2=m-1,x1x2=n-2,
∴m-1<0,n-2>0,
解得:m<1,n>2.
∴x2<3x1,
∵x1<0,
∴x2<0.
∵x1,x2是关于x的一元二次方程x2+x+n-2=mx(x2+(1-m)x+n-2=0)的两个实数根,
∴x1+x2=m-1,x1x2=n-2,
∴m-1<0,n-2>0,
解得:m<1,n>2.
点评:本题考查了一元二次方程根的分布,熟悉一元二次方程根与系数的关系是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
以2、4为两边长的三角形的第三边长是方程x2-7x+10=0的根,则这个三角形的周长为( )
| A、8 | B、11 |
| C、11或8 | D、以上都不对 |
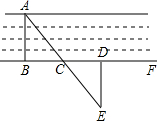 要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )
要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )| A、边角边 | B、角边角 |
| C、边边边 | D、边边角 |
下面说法正确的是( )
| A、0不是自然数 |
| B、0是最小的有理数 |
| C、0是最小的整数 |
| D、0是绝对值最小的有理数 |
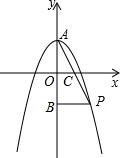 如图,抛物线y=ax2+2与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,若AC=PC,且S△AOC=1,记点A关于x轴的对称点为B.连结BP.
如图,抛物线y=ax2+2与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,若AC=PC,且S△AOC=1,记点A关于x轴的对称点为B.连结BP.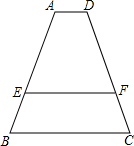 如图,已知AD∥EF∥BC,AD=2,BC=6,AE2=AB•EB,则EF=
如图,已知AD∥EF∥BC,AD=2,BC=6,AE2=AB•EB,则EF=