题目内容
6.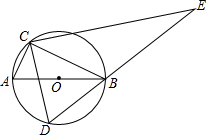 如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若AB=2$\sqrt{5}$,则AC=2,线段CE长度的最大值是4$\sqrt{5}$.
如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若AB=2$\sqrt{5}$,则AC=2,线段CE长度的最大值是4$\sqrt{5}$.
分析 根据tan∠ABC=$\frac{1}{2}$,得到BC=2AC,根据勾股定理求出AC的长,根据当CD最大时,CE长度最大,证明△ACB∽△DCE,求出CE的长.
解答 解:∵tan∠ABC=$\frac{1}{2}$,
∴$\frac{AC}{BC}$=$\frac{1}{2}$,
则BC=2AC,
∵AC2+BC2=AB2,AB=2$\sqrt{5}$,
∴AC=2,
根据题意,当CD最大时,CE长度最大,
则CD为直径,CE为切线,
∴△ACB∽△DCE,
∴$\frac{CD}{CE}$=$\frac{AC}{BC}$,CD=2$\sqrt{5}$,
∴CE=4$\sqrt{5}$.
故答案为:2;4$\sqrt{5}$.
点评 本题考查的是圆周角定理、勾股定理、相似三角形的判定和性质,灵活运用直径所对的圆周角为直角,直径是最长的弦,相似三角形的对应边成比例是解题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
12.在△ABC中,∠C=90°,∠A=60°,AC=1,D在BC上,E在AB上,使得△ADE为等腰直角三角形,∠ADE=90°,则BE的长为( )
| A. | $4-2\sqrt{3}$ | B. | $2-\sqrt{3}$ | C. | $\sqrt{3}-1$ | D. | $\frac{1}{2}(\sqrt{3}-1)$ |
 学校体育运动会的颁奖台放置于校体育馆内,其主视图如图所示,则其左视图是( )
学校体育运动会的颁奖台放置于校体育馆内,其主视图如图所示,则其左视图是( )




 如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度向B点运动,同时动点N自A点出发沿折线AD-DC-CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间的函数关系的是( )
如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度向B点运动,同时动点N自A点出发沿折线AD-DC-CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间的函数关系的是( )



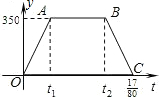 沪杭高速铁路已建成通车,某校研究性学习小组以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若v是关于t的函数,图象为折线O-A-B-C,其中A(t1,350),B(t2,350),C($\frac{17}{80}$,0),四边形OABC的面积为70,则t2-t1=$\frac{3}{16}$.
沪杭高速铁路已建成通车,某校研究性学习小组以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若v是关于t的函数,图象为折线O-A-B-C,其中A(t1,350),B(t2,350),C($\frac{17}{80}$,0),四边形OABC的面积为70,则t2-t1=$\frac{3}{16}$.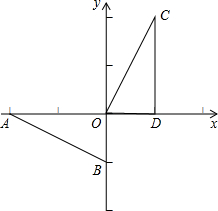 如图,在直角坐标系中,Rt△AOB的两条直角边OA、OB分别在x轴的负半轴、y轴的负半轴上,且OA=2,OB=1.将Rt△AOB绕点O按顺时针方向旋转90°,再把所得的像沿x轴正方向平移1个单位,得△CDO.
如图,在直角坐标系中,Rt△AOB的两条直角边OA、OB分别在x轴的负半轴、y轴的负半轴上,且OA=2,OB=1.将Rt△AOB绕点O按顺时针方向旋转90°,再把所得的像沿x轴正方向平移1个单位,得△CDO.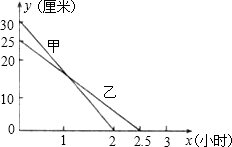 在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题: