题目内容
18.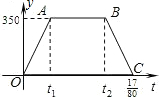 沪杭高速铁路已建成通车,某校研究性学习小组以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若v是关于t的函数,图象为折线O-A-B-C,其中A(t1,350),B(t2,350),C($\frac{17}{80}$,0),四边形OABC的面积为70,则t2-t1=$\frac{3}{16}$.
沪杭高速铁路已建成通车,某校研究性学习小组以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若v是关于t的函数,图象为折线O-A-B-C,其中A(t1,350),B(t2,350),C($\frac{17}{80}$,0),四边形OABC的面积为70,则t2-t1=$\frac{3}{16}$.
分析 如图,由A(t1,350),B(t2,350),可知AB∥OC,则四边形OABC是梯形,t2-t1就是梯形OABC的上底AB,然后根据梯形的面积公式计算即可.
解答 解:∵A(t1,350),B(t2,350),
∴AB∥OC,
∴四边形OABC是梯形,t2-t1就是梯形OABC的上底AB,
∵四边形OABC的面积为70,
即$\frac{1}{2}$(AB+OC)×350=70,
∴$\frac{1}{2}$×(AB+$\frac{17}{80}$)×350=70,
解得:AB=$\frac{3}{16}$,
故t2-t1=AB=$\frac{3}{16}$,
故答案为:$\frac{3}{16}$.
点评 此题考查了学生从图象中读取信息的数形结合能力,用的公式是梯形的面积公式,解题的关键是:判断四边形OABC是梯形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
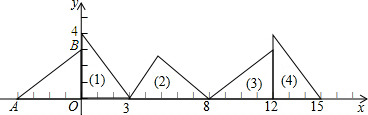
7.在平面直角坐标系中,已知点A(-4,0),B(0,3),对△AOB连续作图所示的旋转变换,依次得到三角形(1),(2),(3),(4)…,那么第(2013)个三角形的直角顶点坐标是(8052,0)

8.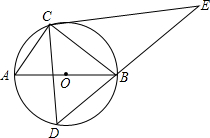 如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
 如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )| A. | 5 | B. | 8 | C. | $\frac{32}{5}$ | D. | $\frac{20}{3}$ |
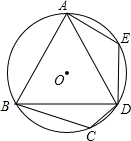 如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=110°.若点E在$\widehat{AD}$上,则∠E=125°.
如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=110°.若点E在$\widehat{AD}$上,则∠E=125°.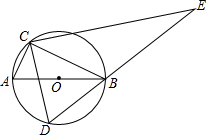 如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若AB=2$\sqrt{5}$,则AC=2,线段CE长度的最大值是4$\sqrt{5}$.
如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若AB=2$\sqrt{5}$,则AC=2,线段CE长度的最大值是4$\sqrt{5}$.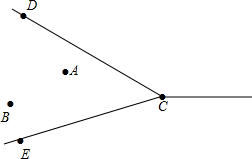 A、B两村坐落在两条相交公路CD、CE内,现计划修建一所小学校,要求学校必须满足下列条件:
A、B两村坐落在两条相交公路CD、CE内,现计划修建一所小学校,要求学校必须满足下列条件: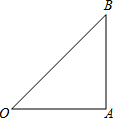 如图,Rt△ABC中,∠OAB=90°,OA=AB=2,
如图,Rt△ABC中,∠OAB=90°,OA=AB=2,