题目内容
12.在△ABC中,∠C=90°,∠A=60°,AC=1,D在BC上,E在AB上,使得△ADE为等腰直角三角形,∠ADE=90°,则BE的长为( )| A. | $4-2\sqrt{3}$ | B. | $2-\sqrt{3}$ | C. | $\sqrt{3}-1$ | D. | $\frac{1}{2}(\sqrt{3}-1)$ |
分析 过点EF作∥AC,交BC于点F,证明△ADC和△DEF全等,得出DF=AC=1,设CD=x,利用平行线分线段成比例定理,列出比例式,列方程解答.
解答 解:过点E作EF作∥AC,交BC于点F,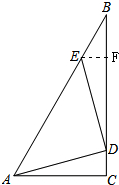
∴∠BFC=∠C=90°,
∵∠C=90°,∠BAC=60°,
∴∠B=30°
∴AB=2AC=2,
在Rt△ABC中,由勾股定理得:CB=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∵△ADE是等腰直角三角形,
∴DE=DA,
∵∠DAC+∠ADC=90°,∠EDF+∠ADC=90°,
∴∠DAC=∠EDF
在△ADC和△DEF中,
$\left\{\begin{array}{l}{∠DAC=∠EDF}\\{∠C=∠EFD=90°}\\{DA=DE}\end{array}\right.$,
∴△ADC≌△DEF(AAS),
∴DF=AC=1,
设CD=x,所以EF=x,BF=$\sqrt{3}$-1-x
∵EF∥AC
∴$\frac{EF}{AC}$=$\frac{BF}{BC}$,即$\frac{x}{1}$=$\frac{\sqrt{3}-1-x}{\sqrt{3}}$,
解得:x=2-$\sqrt{3}$,
∴BE=2x=4-2$\sqrt{3}$.
故选A
点评 此题考查了全等三角形的性质和判定、勾股定理、平行线分线段成比例定理,解题的关键是添加辅助线构造全等三角形.

练习册系列答案
相关题目
2.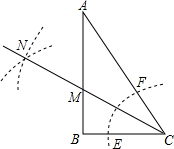 Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于$\frac{1}{2}$EF为半径画弧,两弧交于点N,若BC=$\sqrt{3}$,则点M到AC的距离是( )
Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于$\frac{1}{2}$EF为半径画弧,两弧交于点N,若BC=$\sqrt{3}$,则点M到AC的距离是( )
 Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于$\frac{1}{2}$EF为半径画弧,两弧交于点N,若BC=$\sqrt{3}$,则点M到AC的距离是( )
Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于$\frac{1}{2}$EF为半径画弧,两弧交于点N,若BC=$\sqrt{3}$,则点M到AC的距离是( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 3 |
17.某足球协会举办了一次足球联赛,其记分规则如下表:
当比赛进行到第二轮结束(每队均需比赛12场)时,A队共积19分,问A队胜,平,负各几场?
| 胜一场 | 平一场 | 负一场 | |
| 积分 | 3 | 1 | 0 |
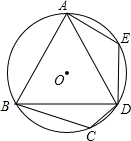 如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=110°.若点E在$\widehat{AD}$上,则∠E=125°.
如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=110°.若点E在$\widehat{AD}$上,则∠E=125°.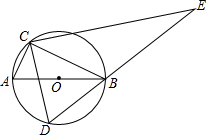 如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若AB=2$\sqrt{5}$,则AC=2,线段CE长度的最大值是4$\sqrt{5}$.
如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若AB=2$\sqrt{5}$,则AC=2,线段CE长度的最大值是4$\sqrt{5}$.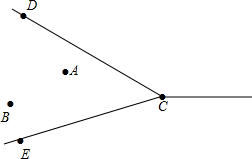 A、B两村坐落在两条相交公路CD、CE内,现计划修建一所小学校,要求学校必须满足下列条件:
A、B两村坐落在两条相交公路CD、CE内,现计划修建一所小学校,要求学校必须满足下列条件: