题目内容
6.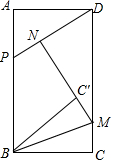 如图,在矩形ABCD中,AB=$\sqrt{3}$AD,点P在线段AB上,满足PB=PD,点M在射线CD上,点C关于直线BM的对称点为点C′,连接C′B、C′M,射线MC′与射线DP交于点N.
如图,在矩形ABCD中,AB=$\sqrt{3}$AD,点P在线段AB上,满足PB=PD,点M在射线CD上,点C关于直线BM的对称点为点C′,连接C′B、C′M,射线MC′与射线DP交于点N.(1)求证:∠PDC=60°;
(2)求证:当M在线段CD上时,∠MBN=60°;
(3)已知AB=9,请直接写出当点M在CD边的延长线上时,线段NC′与NP的数量关系:NP-NC'=3.
分析 (1)先设出AP,表示出BP,PD,进而用勾股定理求出x=$\frac{\sqrt{3}}{3}$AD,再用三角函数求出∠ADP=30°,即可得出结论;
(2)先求出∠CBH=120°,再判断出Rt△BHN≌Rt△BC'N,得出∠HBN=∠C'BN,进行代换即可得出结论;
(3)同(2)的方法判断出HN=NC',再求出PH,即可得出结论.
解答 解:(1)设AP=x,
∴PB=AB-AP=AB-x,
∵AB=$\sqrt{3}$AD,
∴BP=$\sqrt{3}$AD-x,
∵PB=PD,
∴PD=$\sqrt{3}$AD-x,
∴四边形ABCD是矩形,
∴BC=AD,∠C=∠A=∠ABC∠ADC=90°,
在Rt△ADP中,AP=x,PD=$\sqrt{3}$AD-x,
根据勾股定理得,AD2+AP2=PD2,
∴AD2+x2=($\sqrt{3}$AD-x)2,
∴x=$\frac{\sqrt{3}}{3}$AD,
∴tan∠ADP=$\frac{AP}{AD}$=$\frac{\sqrt{3}}{3}$,
∴∠ADP=30°,
∴∠PDC=90°-∠ADP=60°;
(2)如图1,
过点B作BH⊥DP交DP的延长线于H,
由(1)知,BP=$\sqrt{3}$AD-x=$\frac{2\sqrt{3}}{3}$AD,∠ADP=30°,
∴∠BPH=∠APD=60°,BH=AD=BC,
∴∠PBH=30°,
∴∠CBH=120°,
∵点C关于直线BM的对称点为点C′,
∴BC'=BC=AD,∠CBM=∠C'BM,∠BC'M=∠C=90°,
∴∠BC'N=90°,
在Rt△BHN和Rt△BC'N中,$\left\{\begin{array}{l}{BH=BC'}\\{BN=BN}\end{array}\right.$,
∴Rt△BHN≌Rt△BC'N,
∴∠HBN=∠C'BN,
∴∠CBH=∠HBN+∠C'BN+∠C'BM+∠CBM=120°,
∴∠MBN=∠C'BN+∠C'BM=$\frac{1}{2}$(∠HBN+∠C'BN+∠C'BM+∠CBM)=60°,
即:当M在线段CD上时,∠MBN=60°;
(3)如图3,∵AB=$\sqrt{3}$AD=9,
∴AD=3$\sqrt{3}$, 过点B作BH⊥DP交DP的延长线于H,
过点B作BH⊥DP交DP的延长线于H,
由(1)知,BP=$\sqrt{3}$AD-x=$\frac{2\sqrt{3}}{3}$AD=6,∠ADP=30°,
∴∠BPH=∠APD=60°,BH=AD=BC,
∴∠PBH=30°,
∴∠CBH=120°,
∵点C关于直线BM的对称点为点C′,
∴BC'=BC=AD,∠CBM=∠C'BM,∠BC'M=∠C=90°,
∴∠BC'N=90°,
在Rt△BHN和Rt△BC'N中,$\left\{\begin{array}{l}{BH=BC'}\\{BN=BN}\end{array}\right.$,
∴Rt△BHN≌Rt△BC'N,
∴HN=NC',在Rt△BPH中,∠BPH=60°,BP=6,
∴PH=3,
∴NP=PH+HN=3+NH=3+NC',
∴NP-NC'=3.
故答案为:NP-NC'=3.
点评 此题是四边形综合题,主要考查了对称的性质,全等三角形的判定和性质,勾股定理,含30°的直角三角形的性质,解本题的关键是判断出Rt△BHN≌Rt△BC'N,难点是(3)作出图形,是一道很好的中考常考题.

 有理数a、b、c在数轴上的位置如图所示,化简|a-b|+|c-a|-|b-c|的结果是( )
有理数a、b、c在数轴上的位置如图所示,化简|a-b|+|c-a|-|b-c|的结果是( )| A. | -2a | B. | -2b | C. | -2a-2b | D. | 2a-2b |
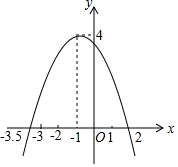 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点(2,0)和(-3.5,0),顶点为(-1,4),根据图象直接写出下列答案.
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点(2,0)和(-3.5,0),顶点为(-1,4),根据图象直接写出下列答案. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①abc<0;②b2-4ac>0;③m>2;④当x<0时,y随x的增大而增大.其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①abc<0;②b2-4ac>0;③m>2;④当x<0时,y随x的增大而增大.其中正确结论的个数是( )
 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的个数为( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的个数为( )