题目内容
8.已知在△ABC中,AB=14,BC=13,tanB=$\frac{12}{5}$,则sinA的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{7}{25}$ | D. | $\frac{56}{65}$ |
分析 作CD⊥AB,由tanB=$\frac{CD}{BD}$=$\frac{12}{5}$及BC=13利用勾股定理求得BD=5、CD=12,即可知AD=9,根据勾股定理求得AC的值即可得出答案.
解答 解:如图,过点C作CD⊥AB于点D,
在Rt△BCD中,∵tanB=$\frac{CD}{BD}$=$\frac{12}{5}$,
∴设CD=12x,BD=5x,
∵BC=13,
∴由BC2=BD2+CD2可得132=(5x)2+(12x)2,
解得:x=-1(舍)或x=1,
则BD=5,CD=12,
∵AB=14,
∴AD=9,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{{9}^{2}+1{2}^{2}}$=15,
∴sinA=$\frac{CD}{AC}$=$\frac{12}{15}$=$\frac{4}{5}$,
故选:B.
点评 本题主要考查解直角三角形,熟练掌握勾股定理和三角函数并结合题意构建直角三角形是解题的关键.

练习册系列答案
相关题目
9.已知x+y=-5,xy=6,则x2+y2的值是( )
| A. | 1 | B. | 13 | C. | 17 | D. | 25 |
6.已知$\root{3}{177}$≈5.615,由此可见下面等式成立的是( )
| A. | $\root{3}{0.177}$≈0.5615 | B. | $\root{3}{0.0177}$≈0.5615 | C. | $\root{3}{1.77}$≈0.5165 | D. | $\root{3}{17.7}$≈56.15 |
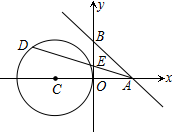 如图,在平面直角坐标系xOy中,A(2,0)、B(0,2),C的圆心为点C(-2,0),半径为2.若D是C上一动点,线段DA与y轴交于点E,则△ABE的面积s的取值范围是2-$\frac{2\sqrt{3}}{3}$≤S≤2+$\frac{2\sqrt{3}}{3}$.
如图,在平面直角坐标系xOy中,A(2,0)、B(0,2),C的圆心为点C(-2,0),半径为2.若D是C上一动点,线段DA与y轴交于点E,则△ABE的面积s的取值范围是2-$\frac{2\sqrt{3}}{3}$≤S≤2+$\frac{2\sqrt{3}}{3}$.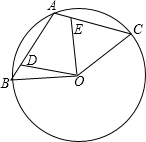 已知A、B、C是圆O上的三个点,其中点A是弧BC的中点,连接AB、AC,点D、E分别在弦AB、AC上,且满足AD=CE.
已知A、B、C是圆O上的三个点,其中点A是弧BC的中点,连接AB、AC,点D、E分别在弦AB、AC上,且满足AD=CE.
 画图并填空:如图,方格纸中每个小正方形的边长都为1,在方格纸中将△ABC经过一次平移后得到△A′B′C′,图中标出来点A,点B′、点C和它的对应点C′.
画图并填空:如图,方格纸中每个小正方形的边长都为1,在方格纸中将△ABC经过一次平移后得到△A′B′C′,图中标出来点A,点B′、点C和它的对应点C′. 如图,在正方形ABCD内有一折线段,其中AE丄EF,EF丄FC,并且AE=3,EF=4,FC=5,则正方形ABCD的外接圆的半径是4$\sqrt{5}$.
如图,在正方形ABCD内有一折线段,其中AE丄EF,EF丄FC,并且AE=3,EF=4,FC=5,则正方形ABCD的外接圆的半径是4$\sqrt{5}$.