题目内容
7．
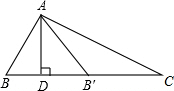如图，△ABC中，∠B=2∠C，AD是BC上的高，沿AD所在直线将△ABD翻折，点B落在B′处．（1）点B′在DC上吗？为什么？并画出点B′；
（2）线段AB、BD、CD之间有何等量关系？
分析 （1）由于AD⊥BC，沿AD所在直线将△ABD翻折，点B落在B′处，则∠ADB=∠ADB′=90°，所以∠ADB+∠ADB′=180°，所以点B′在DC上．
（2）AB+BD=DC；根据三角形外角等于和它不相邻的两内角和，知∠AB′C=∠C+∠B′AC，根据折叠的性质，∠B=∠AB′D，又∠B=2∠C，所以∠C=∠CAB′，故AB′=CB′，根据折叠的性质可知，BD=B′D，AB=AB′，所以AB+BD=DC．
解答 解：（1）∵AD⊥BC，
∴∠ADB=∠ADC=90°
∵沿AD所在直线将△ABD翻折，点B落在B′处，
∴∠ADB=∠ADB′=90°，
∴所以∠ADB+∠ADB′=180°，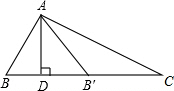
∴点B′在DC上．
（2）AB+BD=DC；
根据折叠的性质，∠B=∠AB′D，
∵∠AB′C=∠C+∠B′AC，∠B=2∠C，
∴∠C=∠CAB′，
∴AB′=CB′，
根据折叠的性质可知，BD=B′D，AB=AB′，
∴AB+BD=B′C+DB′=DC．
点评 此题主要考查了折叠的性质以及等腰三角形的判定和性质、三角形的内角和定理以及三角形外角和定理，题目的综合性很强，难度不大，解题的关键是利用方程思想解决几何图形问题．
练习册系列答案
相关题目
18．将6个边长是1的正方形无缝隙铺成一个矩形，则这个矩形的对角线长等于（ ）
| A． | $\sqrt{37}$ | B． | $\sqrt{13}$ | C． | $\sqrt{37}$、$\sqrt{13}$ | D． | $\sqrt{37}$、$\sqrt{13}$、5 |
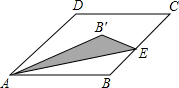如图，已知在周长为20的菱形ABCD中，∠C=45°，点E是线段BC上一点，将△ABE沿AE所在直线翻折，使点B落在B′上，则在点E沿B→C→D运动的过程中，点B′运动的路径长是$\frac{5π}{4}$．
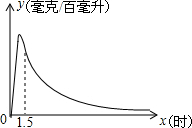实验数据显示：一般成人喝半斤低度白酒后，1.5小时内（包括1.5小时）其血液中酒精含量y（毫克/百毫升）与时间x（时）的关系可近似地用二次函数y=-200x2+400x表示；1.5小时后（包括1.5小时）y与x可近似地用反比例函数y=$\frac{k}{x}$（k＞0）表示（如图所示）．
19．图1中的摩天轮可抽象成一个圆，圆上一点离地面的高度y（m）与旋转时间x（min）之间的关系如图2所示．
（1）根据图2填表：
（2）变量y是x的函数吗？为什么？
（3）根据图中的信息，请写出摩天轮的直径．
（1）根据图2填表：
| x（min） | 0 | 3 | 6 | 8 | 12 | … |
| y（m） | 5 | 70 | 5 | 54 | 5 | … |
（3）根据图中的信息，请写出摩天轮的直径．
如图，在△ABC中，DE∥BC，$\frac{AD}{AB}=\frac{1}{3}$，DE=6，则BC的长是18．