题目内容
2.如图,AB为半圆的直径,C为$\widehat{AB}$的中点,点E为$\widehat{CB}$上一点.(1)若$\widehat{CE}$=$\widehat{BE}$,求$\frac{BE}{AF}$的值;
(2)若tan∠CBE=$\frac{1}{2}$,求$\frac{EF}{AF}$的值.

分析 (1)如图1,连接AC,CE,作E作ED⊥BC于D,由$\widehat{CE}$=$\widehat{BE}$,得到CE=DE,于是△BCE是等腰三角形,BD=CD=$\frac{1}{2}$BC,根据C为$\widehat{AB}$的中点,AB为半圆的直径,得到△ABC是等腰直角三角形,推出△ACF∽△BDE,于是得到结果;
(2)如图2,连接AC,作E作ED⊥BC于D,由AB为半圆的直径,得到∠C=∠AEB=90°,推出∠DEF=∠1=∠2,于是tan∠DEF=tan∠1=tan∠2,即$\frac{DF}{DE}=\frac{CF}{AC}=\frac{DE}{BD}=\frac{1}{2}$,得到DE=2DF,AC=2CF,BD=2DE,得出△ACF∽△EDF,求出结果.
解答 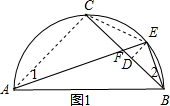 解:(1)如图1,连接AC,CE,作E作ED⊥BC于D,
解:(1)如图1,连接AC,CE,作E作ED⊥BC于D,
∵$\widehat{CE}$=$\widehat{BE}$,∴CE=BE,
∴△BCE是等腰三角形,
∴BD=CD=$\frac{1}{2}$BC,
∵C为$\widehat{AB}$的中点,
AB为半圆的直径,
∴△ABC是等腰直角三角形,
∴AC=CB,∠ACB=90°,
∵∠1=∠2,
∴△ACF∽△BDE,
∴$\frac{BE}{AF}=\frac{BD}{AC}=\frac{1}{2}$;
(2)如图2,连接AC,作E作ED⊥BC于D,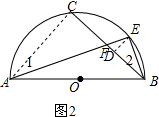
∵AB为半圆的直径,
∴∠C=∠AEB=90°,
∴AC∥DE,
∴∠DEF=∠1=∠2,
∴tan∠DEF=tan∠1=tan∠2,即$\frac{DF}{DE}=\frac{CF}{AC}=\frac{DE}{BD}=\frac{1}{2}$,∴DE=2DF,AC=2CF,BD=2DE,
∴BD=4DF,
∴BF=5DF,
∵∠C=∠EDF=90°,∠AFC=∠DFE,
∴△ACF∽△EDF,
∴$\frac{EF}{AF}$=$\frac{DF}{CF}$=$\frac{1}{5}$.
点评 本题考查了相似三角形的判定和性质,垂径定理,三角函数,正确的作出辅助线是解题的关键.

| 商铺的面积(m2) | 购买费用(万元) | 装修费用(万元) |
| 1 | 1.8 | 0.3 |
(2)购买商铺后,小王准备经营童鞋专卖店,已知专卖店代理的某品牌童鞋的进价为每双40元,该品牌童鞋日销售量y(双)与销售单价x(元/双)之间的关系式为:
y=$\left\{\begin{array}{l}{-2x+140(40≤x≤58)}\\{-x+82(58<x≤71)}\end{array}\right.$
①求他的销售利润w(元)与销售单价x(元/双)之间的函数关系式.
②小王每月需向银行还贷2075元,另童鞋店每月需缴纳水电费、营业税等固定费用3000元,通过计算判断,小王每月(按30天计算)能否有盈余?如果有,最多盈余多少元?(盈余=销售利润-固定费用-银行贷款)
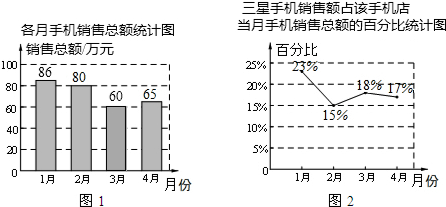
| A. | 4月份三星手机销售额为65万元 | |
| B. | 4月份三星手机销售额比3月份有所上升 | |
| C. | 4月份三星手机销售额比3月份有所下降 | |
| D. | 3月份与4月份的三星手机销售额无法比较,只能比较该店销售总额 |
 附加题
附加题
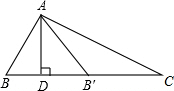 如图,△ABC中,∠B=2∠C,AD是BC上的高,沿AD所在直线将△ABD翻折,点B落在B′处.
如图,△ABC中,∠B=2∠C,AD是BC上的高,沿AD所在直线将△ABD翻折,点B落在B′处.
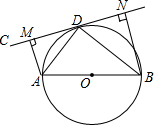 如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,BN⊥CD于N.
如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,BN⊥CD于N.