题目内容
12.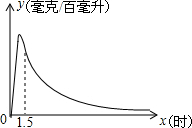 实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示).
实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示).(1)喝酒后多长时间血液中的酒精含量达到最大值?最大值为多少?
(2)求k的值.
(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
分析 (1)利用y=-200x2+400x=-200(x-1)2+200确定最大值;
(2)直接带入x=1.5求值即可;
(3)求出x=11时,y的值,进而得出能否驾车去上班.
解答 解:(1)y=-200x2+400x=-200(x-1)2+200,
∴x=1时血液中的酒精含量达到最大值,最大值为200(毫克/百毫升);
(2)当x=1.5时,y=-200x2+400x=-200×2.25+400×1.5=150,
∴k=1.5×150=225;
(3)不能驾车上班;
理由:∵晚上20:00到第二天早上7:00,一共有11小时,
∴将x=11代入y=$\frac{225}{x}$,则y=$\frac{225}{11}$>20,
∴第二天早上7:00不能驾车去上班.
点评 此题主要考查了二次函数综合应用,根据图象得出正确信息是解题关键,能够从实际问题中抽象出二次函数模型是解答的重点.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
3.某大学生利用暑假开展了30天的社会实践活动,参与了某超市的经营,了解到某成本为10元/件的商品杂x天销售的相关信息,如表表示:
设该超市在第x天销售这种商品获得的利润为y元.
(1)求y关于x的函数关系式;
(2)在这30天中,该超市销售这种商品第几天的利润最大?最大利润是多少?
| 销售量p(件) | P=40-x |
| 销售单价q(元/件) | 当1≤x≤20时,q=20+x 当20<x≤30时,q=40 |
(1)求y关于x的函数关系式;
(2)在这30天中,该超市销售这种商品第几天的利润最大?最大利润是多少?
1.要使二次根式$\sqrt{x-2}$有意义,x必须满足( )
| A. | x≤2 | B. | x≥2 | C. | x>2 | D. | x<2 |
2.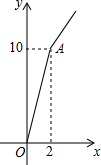 某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10),请你结合表格和图象:
某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10),请你结合表格和图象:
(1)指出付款金额和购买量哪个变量是函数的自变量x,并写出表中a、b的值;
(2)求出当x>2时,y关于x的函数解析式;
(3)甲农户将8.8元钱全部用于购买玉米种子,乙农户购买了4165克该玉米种子,分别计算他们的购买量和付款金额.
 某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10),请你结合表格和图象:
某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10),请你结合表格和图象:| 付款金额 | a | 7.5 | 10 | 12 | b |
| 购买量(千克) | 1 | 1.5 | 2 | 2.5 | 3 |
(2)求出当x>2时,y关于x的函数解析式;
(3)甲农户将8.8元钱全部用于购买玉米种子,乙农户购买了4165克该玉米种子,分别计算他们的购买量和付款金额.
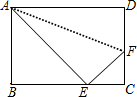 如图所示,将矩形ABCD沿直线AF折叠,点D恰好落在边BC上的点E处,若AB=8cm,BC=10cm,求EF的长.
如图所示,将矩形ABCD沿直线AF折叠,点D恰好落在边BC上的点E处,若AB=8cm,BC=10cm,求EF的长.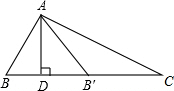 如图,△ABC中,∠B=2∠C,AD是BC上的高,沿AD所在直线将△ABD翻折,点B落在B′处.
如图,△ABC中,∠B=2∠C,AD是BC上的高,沿AD所在直线将△ABD翻折,点B落在B′处.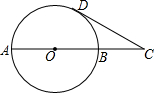 如图,已知AB是⊙O的一条直径,延长AB至C点,使AC=3BC,CD与⊙O相切于D点.若CD=$\sqrt{3}$,则劣弧AD的长为$\frac{2}{3}$π.
如图,已知AB是⊙O的一条直径,延长AB至C点,使AC=3BC,CD与⊙O相切于D点.若CD=$\sqrt{3}$,则劣弧AD的长为$\frac{2}{3}$π.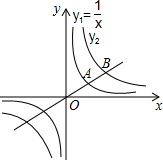 如图,过原点O的直线与反比例函数y1,y2的图象在第一象限内分别交于点A,B,且A为OB的中点,若函数y1=$\frac{1}{x}$,则y2与x的函数表达式是y2=$\frac{4}{x}$.
如图,过原点O的直线与反比例函数y1,y2的图象在第一象限内分别交于点A,B,且A为OB的中点,若函数y1=$\frac{1}{x}$,则y2与x的函数表达式是y2=$\frac{4}{x}$.