题目内容
2.从-1,0,2,1四个数中任意取两个数组成一个点坐标,那么这个点落在以原点为圆心,半径为2的圆内的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 首先确定四个数组成的点的情况,然后确定点落在以原点为圆心,半径为2的圆内的情况,从而利用概率公式计算概率即可.
解答 解:-1,0,2,1四个数中任意取两个数组成一个点坐标,可能有(-1,0),(-1,2),(-1,1),(0,2),(0,1),(2,1)共6种情况,
落在以原点为圆心,半径为2的圆内的有(-1,0),(-1,1),(0,2),(0,1)共3种情况,
所以这个点落在以原点为圆心,半径为2的圆内的概率是$\frac{3}{6}$=$\frac{1}{2}$,
故选C.
点评 本题考查了几何概率的知识,解题的关键是能够将所有等可能的结果列举出来,难度不大.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
12.将104.6402精确到0.01为( )
| A. | 104 | B. | 104.6 | C. | 104.64 | D. | 104.640 |
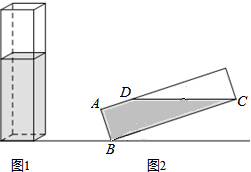
 如图,M点到小河的距离MA=20米,N点到小间的距离NB=40米,且AB=80米,现在菲菲要从M点走到河边某处打水去N点,她至少要走100米的路.
如图,M点到小河的距离MA=20米,N点到小间的距离NB=40米,且AB=80米,现在菲菲要从M点走到河边某处打水去N点,她至少要走100米的路.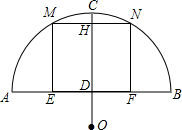 如图,某地有一座圆弧形拱桥,桥下水面宽度AB为12米,拱顶离水面的高CD为3米,现有一艘宽9米,船舱顶部为长方形,并且高出水面1.8米的货船要经过这里,此货船能顺利通过这座桥吗?(此图仅供参考)
如图,某地有一座圆弧形拱桥,桥下水面宽度AB为12米,拱顶离水面的高CD为3米,现有一艘宽9米,船舱顶部为长方形,并且高出水面1.8米的货船要经过这里,此货船能顺利通过这座桥吗?(此图仅供参考)