题目内容
13.一长方体容器(如图1),长、宽均为2,高为8,里面盛有水,水面高为5,若沿底面一棱进行旋转倾斜,倾斜后的长方体容器的主视图如图2所示,若倾斜容器使水恰好倒出容器,则CD=2$\sqrt{10}$.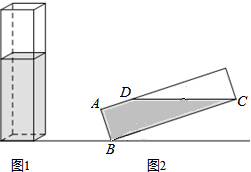
分析 设DE=x,则AD=8-x,由长方体容器内水的体积得出方程,解方程求出DE,再由勾股定理求出CD即可.
解答 解:如图所示:
设DE=x,则AD=8-x,
根据题意得:$\frac{1}{2}$(8-x+8)×2×2=2×2×5,
解得:x=6,
∴DE=6,
∵∠E=90°,
由勾股定理得:CD=$\sqrt{D{E}^{2}+C{E}^{2}}$=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$,
故答案为:2$\sqrt{10}$.
点评 本题考查了勾股定理的应用、长方体的体积、梯形的面积的计算方法;熟练掌握勾股定理,由长方体容器内水的体积得出方程是解决问题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
3.下列方程组是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}2x-y=0\\ 3x+2y=1\end{array}\right.$ | B. | $\left\{\begin{array}{l}2x-3y=-3\\ 3z+y=1\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x-y=4\\{x^2}-{y^2}=12\end{array}\right.$ | D. | $\left\{\begin{array}{l}2x-y=0\\ \frac{1}{x}+\frac{1}{y}=4\end{array}\right.$ |
2.从-1,0,2,1四个数中任意取两个数组成一个点坐标,那么这个点落在以原点为圆心,半径为2的圆内的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 如图,已知△ABC是等边三角形,D、E 分别在边BC、AC上,且CD=CE,连结DE并延长至点F,使EF=AE,连结AF、BE和CF.
如图,已知△ABC是等边三角形,D、E 分别在边BC、AC上,且CD=CE,连结DE并延长至点F,使EF=AE,连结AF、BE和CF. 如图,已知△ABC的周长为42,面积为84,画出△ABC的内切圆,并求其半径.
如图,已知△ABC的周长为42,面积为84,画出△ABC的内切圆,并求其半径. 如图,⊙O是△ABC的内切圆,D、E、F为切点,AB=14cm,BC=18cm,AC=20cm,求AE、BF、CD的长.
如图,⊙O是△ABC的内切圆,D、E、F为切点,AB=14cm,BC=18cm,AC=20cm,求AE、BF、CD的长.