题目内容
14．如图，用围棋子按下面的规律摆图案，则摆第n个图案需要围棋子的个数是5n+2．
分析 由图可知：摆第1个图案需要围棋子的个数是1+2×3=7，摆第2个图案需要围棋子的个数是2+2×5=12，摆第3个图案需要围棋子的个数是3+2×7=17，…由此得出摆第n个图案需要围棋子的个数是n+2（2n+1）=5n+2．
解答 解：∵摆第1个图案需要围棋子的个数是1+2×3=7，
摆第2个图案需要围棋子的个数是2+2×5=12，
摆第3个图案需要围棋子的个数是3+2×7=17，
…
∴摆第n个图案需要围棋子的个数是n+2（2n+1）=5n+2．
故答案为：5n+2．
点评 此题考查图形的变化规律，把图形分组，两侧和中间，找出棋子个数的变化规律，找出规律，解决问题．
练习册系列答案
相关题目
如图，⊙O是△ABC的内切圆，D、E、F为切点，AB=14cm，BC=18cm，AC=20cm，求AE、BF、CD的长．
2．从-1，0，2，1四个数中任意取两个数组成一个点坐标，那么这个点落在以原点为圆心，半径为2的圆内的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
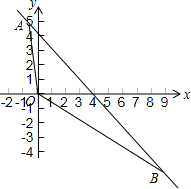如图所示，已知直线y=kx+b过点A（-1，5），且平行于直线y=-x+2．
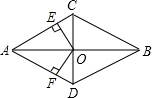在四边形ABCD中．AB与CD互相垂直平分，垂足为O．
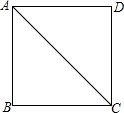如图，正方形ABCD中边长为2cm，以B为圆心，$\sqrt{2}$cm为半径作圆，试判断⊙B与AC的位置关系并证明你的结论．