题目内容
17.二次函数y=x2-2x-1的图象在x轴上截得的线段长为2$\sqrt{2}$.分析 通过解方程x2-2x-1=0可得到抛物线与x轴的两交点坐标,然后计算两交点间的距离即可.
解答 解:当y=0时,x2-2x-1=0,
x2-2x+1=2,
(x-1)2=2,
解得x1=1+$\sqrt{2}$,x2=1-$\sqrt{2}$,
所以抛物线与x轴的两交点坐标为(1-$\sqrt{2}$,0),(1+$\sqrt{2}$,0),
所以抛物线在x轴上截得的线段长=1+$\sqrt{2}$-(1-$\sqrt{2}$)=2$\sqrt{2}$.
故答案为$2\sqrt{2}$.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题可转化为解关于x的一元二次方程.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
12.若二次函数y=-x2+6x+c的图象过点A(-1,y1),B(1,y2),C(4,y3)三点,则y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y2>y1 | D. | y3>y1>y2 |
2.从-1,0,2,1四个数中任意取两个数组成一个点坐标,那么这个点落在以原点为圆心,半径为2的圆内的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 如图,⊙O是△ABC的内切圆,D、E、F为切点,AB=14cm,BC=18cm,AC=20cm,求AE、BF、CD的长.
如图,⊙O是△ABC的内切圆,D、E、F为切点,AB=14cm,BC=18cm,AC=20cm,求AE、BF、CD的长.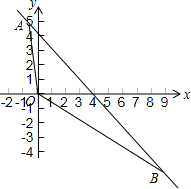 如图所示,已知直线y=kx+b过点A(-1,5),且平行于直线y=-x+2.
如图所示,已知直线y=kx+b过点A(-1,5),且平行于直线y=-x+2.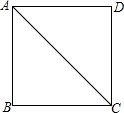 如图,正方形ABCD中边长为2cm,以B为圆心,$\sqrt{2}$cm为半径作圆,试判断⊙B与AC的位置关系并证明你的结论.
如图,正方形ABCD中边长为2cm,以B为圆心,$\sqrt{2}$cm为半径作圆,试判断⊙B与AC的位置关系并证明你的结论.