题目内容
3.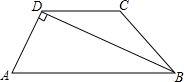 如图,等腰梯形ABCD,AB∥DC,AB=2,∠ADB=90°.
如图,等腰梯形ABCD,AB∥DC,AB=2,∠ADB=90°.(1)试求等腰梯形ABCD的周长y与腰长x之间的函数关系式.
(2)当腰长等于多少时,梯形ABCD的周长有最大值?最大值是多少?
分析 (1)取AB的中点O,作OE⊥AD,DF⊥AO,垂足分别为E、F,根据平行线的判定得到OE∥BD,由三角形的中位线的性质得到AE=$\frac{1}{2}$AD=$\frac{1}{2}$x,由三角形相似得相似比,用x表示AF的长,根据CD=AB-2AF表示等腰梯形的上底,可求梯形的周长;
(2)把(1)中梯形周长的表达式配方,可求周长的最大值.
解答  解:(1)取AB的中点O,过O作OE⊥AD于E,DF⊥AO于F,
解:(1)取AB的中点O,过O作OE⊥AD于E,DF⊥AO于F,
∵∠ADB=90°,
∴OE∥BD,
∴AE=$\frac{1}{2}$AD=$\frac{1}{2}$x,
易证Rt△ADF∽Rt△AOE,
∴$\frac{AF}{AE}=\frac{AD}{AO}$,即$\frac{AF}{\frac{1}{2}x}$=$\frac{x}{1}$,解得AF=$\frac{1}{2}$x2,
∴CD=AB-2AF=2-x2,
∴y=2x+2+2-x2=-x2+2x+4;
(2)∵y=-x2+2x+4=-(x-1)2+5,
∴x=1时,周长最大为5.
点评 本题考查了等腰梯形的性质,二次函数在求梯形周长最值中的运用.关键是利用三角形相似求梯形的上底.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
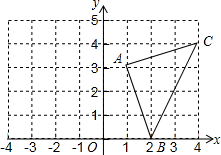 如图,A(1,3),B(2,0),C(4,4).
如图,A(1,3),B(2,0),C(4,4). 如图,AD⊥CD,AB=13,BC=12,CD=4,AD=3,∠CAB=α,求∠B.(用α表示)
如图,AD⊥CD,AB=13,BC=12,CD=4,AD=3,∠CAB=α,求∠B.(用α表示) 用反证法证明:如图,D、E分别是△ABC的边AB.AC上的点,连接CD,BE.求证:CD与BE不能互相平分.
用反证法证明:如图,D、E分别是△ABC的边AB.AC上的点,连接CD,BE.求证:CD与BE不能互相平分. 如图,在?ABCD中,A(1,0),B(0,-2),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,D在y轴上,若?ABCD的面积为6,求k的值.
如图,在?ABCD中,A(1,0),B(0,-2),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,D在y轴上,若?ABCD的面积为6,求k的值.