题目内容
8.在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+3的图象与x轴交于点A,与y轴交于点B,坐标原点为点O,△AOB的外心和内心之间的距离为$\frac{\sqrt{5}}{2}$.分析 根据一次函数解析式求出OB、OA,根据勾股定理求出AB,根据直角三角形的性质求出内切圆的半径、外心的坐标,根据勾股定理计算即可.
解答 解: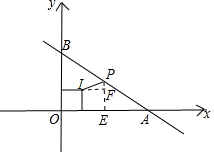 对于y=-$\frac{3}{4}$x+3,
对于y=-$\frac{3}{4}$x+3,
当x=0时,y=3,
y=0时,x=4,
∴OA=4,OB=3,
由勾股定理得,AB=5,
∴△AOB的内切圆的半径=$\frac{3+4-5}{2}$=1,△AOB的外心P在斜边AB的中点,
则点P的坐标为(2,$\frac{3}{2}$),
作PE⊥x轴于E,IF⊥PE于F,
则IF=1,PF=$\frac{1}{2}$,
∴IP=$\sqrt{I{F}^{2}+P{F}^{2}}$=$\frac{\sqrt{5}}{2}$,
故答案为:$\frac{\sqrt{5}}{2}$.
点评 本题考查的是一次函数图象上点的坐标特征、三角形内切圆和内心、外接圆和外心,掌握直角三角形的性质、灵活运用勾股定理是解题的关键.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
20.已知二次函数y=-(x-h)2+1(为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为-5,则h的值为( )
| A. | 3-$\sqrt{6}$或1+$\sqrt{6}$ | B. | 3-$\sqrt{6}$或3+$\sqrt{6}$ | C. | 3+$\sqrt{6}$或1-$\sqrt{6}$ | D. | 1-$\sqrt{6}$或1+$\sqrt{6}$ |
 一个长方形的周长是12 cm,一边长是x( cm).
一个长方形的周长是12 cm,一边长是x( cm).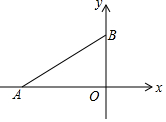 如图,在平面直角坐标系中,A,B两点的坐标分别为(-4,0),(0,3),连接AB.点P在第二象限,若以点P,A,B为顶点的三角形是等腰直角三角形,则点P坐标为(-$\frac{7}{2}$,$\frac{7}{2}$)或(-3,7)或(-7,4).
如图,在平面直角坐标系中,A,B两点的坐标分别为(-4,0),(0,3),连接AB.点P在第二象限,若以点P,A,B为顶点的三角形是等腰直角三角形,则点P坐标为(-$\frac{7}{2}$,$\frac{7}{2}$)或(-3,7)或(-7,4).