题目内容
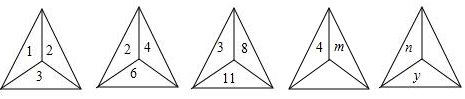
18.内角和与外角和相等的多边形是( )| A. |  | B. |  | C. |  | D. |  |
分析 多边形的外角和是360°,n边形的内角和可以表示成(n-2)•180°,设这个多边形的边数是n,就得到方程,从而求出边数,即可求解.
解答 解:设这个正多边形的边数是n,
则(n-2)•180°=360°,
解得:n=4.
故这个正多边形是四边形.
故选:B.
点评 考查了多边形内角与外角,此题比较简单,只要结合多边形的内角和公式寻求等量关系,构建方程求解.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
3.某农科院要考察某种幼树在一定条件下的移植成活率,下表是这种幼树在移植过程中的一组统计数据:
则该幼树移植成活的概率估计值为0.8(结果精确到0.1).
| 移植总数 | 100 | 400 | 750 | 1500 | 3500 | 7000 | 9000 | 14000 |
| 成活数 | 83 | 314 | 606 | 1197 | 2810 | 5613 | 7194 | 11208 |
| 成活的频率 | 0.83 | 0.785 | 0.808 | 0.798 | 0.803 | 0.802 | 0.799 | 0.801 |
7. 如图,在半径为4的⊙O中,CD是直径,AB是弦,且CD⊥AB,垂足为点E,∠AOB=90°,则阴影部分的面积是( )
如图,在半径为4的⊙O中,CD是直径,AB是弦,且CD⊥AB,垂足为点E,∠AOB=90°,则阴影部分的面积是( )
 如图,在半径为4的⊙O中,CD是直径,AB是弦,且CD⊥AB,垂足为点E,∠AOB=90°,则阴影部分的面积是( )
如图,在半径为4的⊙O中,CD是直径,AB是弦,且CD⊥AB,垂足为点E,∠AOB=90°,则阴影部分的面积是( )| A. | 4π-4 | B. | 2π-4 | C. | 4π | D. | 2π |
8.下列计算的结果是x5的为( )
| A. | x10÷x2 | B. | x6-x | C. | x2•x3 | D. | (x2)3 |
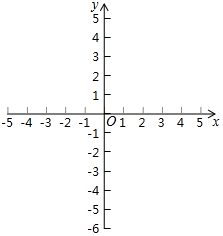 抛物线F与x轴相交于A、B两点(点A在点B的左边),对称轴为直线x=1,顶点C在直线y=x-5上,与y轴相交于点D(0,3).
抛物线F与x轴相交于A、B两点(点A在点B的左边),对称轴为直线x=1,顶点C在直线y=x-5上,与y轴相交于点D(0,3).