题目内容
14.一个不透明的盒子中装有3个红球,2个白球,这些球除颜色外,没有任何其他区别,从这个盒子中同时随机摸出两个球,所有的可能性如下表:| 红球1 | 红球2 | 红球3 | 白球1 | 白球2 | |
| 红球1 | (红1,红2) | (红1,红3) | (红1,白1) | (红1,白2) | |
| 红球2 | (红2,红3) | (红2,白1) | (红2,白2) | ||
| 红球3 | (红3,白1) | (红3,白2) | |||
| 白球1 | (白1,白2) | ||||
| 白球2 |
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{2}{5}$ |
分析 首先根据题意列表,然后求得所有等可能的结果与摸到两个红球的情况,再利用概率公式即可求得答案.
解答 解:列表得:
| 红球1 | 红球2 | 红球3 | 白球1 | 白球2 | |
| 红球1 | (红1,红2) | (红1,红3) | (红1,白1) | (红1,白2) | |
| 红球2 | (红1,红2) | (红2,红3) | (红2,白1) | (红2,白2) | |
| 红球3 | (红1,红3) | (红3,红2) | (红3,白1) | (红3,白2) | |
| 白球1 | (红1,白1) | (红2,白1) | (红3,白1) | (白1,白2) | |
| 白球2 | (红1,白2) | (红2,白2) | (红2,白2) | (白1,白2) |
∴摸到两个红球的概率=$\frac{6}{20}$=$\frac{3}{10}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
5. 如图,半径为2的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是( )
如图,半径为2的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是( )
 如图,半径为2的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是( )
如图,半径为2的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是( )| A. | 18$\sqrt{3}$-6π | B. | 4$\sqrt{3}$-$\frac{4}{3}$π | C. | 9$\sqrt{3}$-$\frac{9}{2}$π | D. | 2$\sqrt{3}$-$\frac{2}{3}$π |
3.某农科院要考察某种幼树在一定条件下的移植成活率,下表是这种幼树在移植过程中的一组统计数据:
则该幼树移植成活的概率估计值为0.8(结果精确到0.1).
| 移植总数 | 100 | 400 | 750 | 1500 | 3500 | 7000 | 9000 | 14000 |
| 成活数 | 83 | 314 | 606 | 1197 | 2810 | 5613 | 7194 | 11208 |
| 成活的频率 | 0.83 | 0.785 | 0.808 | 0.798 | 0.803 | 0.802 | 0.799 | 0.801 |
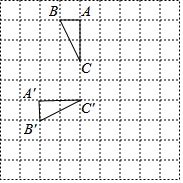 如图,在边长为1的小正方形网格中,将△ABC绕某点旋转到△A'B'C'的位置,则点B运动的最短路径长为$\frac{\sqrt{13}}{2}$π.
如图,在边长为1的小正方形网格中,将△ABC绕某点旋转到△A'B'C'的位置,则点B运动的最短路径长为$\frac{\sqrt{13}}{2}$π.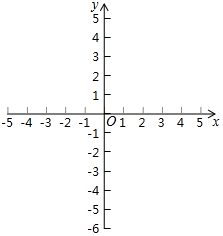 抛物线F与x轴相交于A、B两点(点A在点B的左边),对称轴为直线x=1,顶点C在直线y=x-5上,与y轴相交于点D(0,3).
抛物线F与x轴相交于A、B两点(点A在点B的左边),对称轴为直线x=1,顶点C在直线y=x-5上,与y轴相交于点D(0,3).