题目内容
16. 在平行四边形ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF、BF.
在平行四边形ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF、BF.(1)求证:四边形BFDE是矩形.
(2)若CF=3,BF=4,DF=5,求证:△ADF是等腰三角形.
分析 (1)根据平行四边形的性质可得BE∥DF,再由条件BE=DF,DE⊥AB,根据有一个角是直角的平行四边形是矩形可得结论;
(2)首先根据勾股定理计算出BC的长,根据平行四边形的性质可得AD=5,再由DF=5可得△ADF是等腰三角形.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,即BE∥DF,
又∵BE=DF,DE⊥AB,
∴四边形BFDE是矩形;
(2)∵四边形BFDE是矩形,
∴BF⊥CD,
∴∠BFC=90°,
又∵CF=3,BF=4,
∴BC=5,
又∵四边形ABCD是平行四边形,
∴AD=BC=5,
又∵DF=5,
∴AD=DF=5,
∴△ADF是等腰三角形.
点评 此题主要考查了矩形的判定,以及平行四边形的性质,勾股定理的应用,关键是掌握平行四边形对边平行且相等.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
7.二次函数y1=-3x2,y2=-x2,y3=5x2,它们的图象开口大小由小到大的顺序是( )
| A. | y3<y1<y2 | B. | y3<y2<y1 | C. | y1<y2<y3 | D. | y2<y1<y3 |
1.方程2x-1=0的解是( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
8.下列说法错误的是( )
| A. | 近似数2.50精确到百分位 | B. | 1.45×105精确到千位 | ||
| C. | 近似数13.6亿精确到千万位 | D. | 近似数7000万精确到个位 |
 如图把三角板的直角顶点放在直线b上,若∠1=40°,则当∠2=50度时,a∥b.
如图把三角板的直角顶点放在直线b上,若∠1=40°,则当∠2=50度时,a∥b.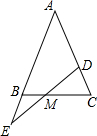 在等腰三角形ABC的腰AC上取一点D,腰AB的延长线上取一点E,使CD=BE,交BC于M,探索能得到的结论,并证明.
在等腰三角形ABC的腰AC上取一点D,腰AB的延长线上取一点E,使CD=BE,交BC于M,探索能得到的结论,并证明.