题目内容
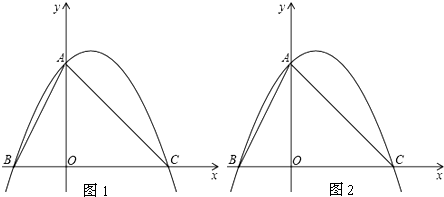
4.二次函数y=kx2-8x+8的图象与x轴有交点,则k的取值范围是k≤2且k≠0.分析 利用△=b2-4ac决定抛物线与x轴的交点个数.△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点,进而得出答案.
解答 解:∵二次函数y=kx2-8x+8的图象与x轴有交点,
∴b2-4ac=64-32k≥0,
解得:k≤2,
故k的取值范围是:k≤2且k≠0.
故答案为:k≤2且k≠0.
点评 此题主要考查了抛物线与x轴的交点,正确把握△的符号与交点个数的关系是解题关键.

练习册系列答案
相关题目
14.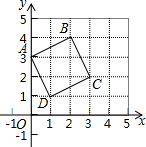 正方形ABCD在坐标系中的位置如图所示,将正方形ABCD沿x轴翻折一次,再沿轴翻折一次,然后向右平移1个单位记作:图形的一次完整变化,图形经历100次这样完整的变化后,点B到达的位置坐标为( )
正方形ABCD在坐标系中的位置如图所示,将正方形ABCD沿x轴翻折一次,再沿轴翻折一次,然后向右平移1个单位记作:图形的一次完整变化,图形经历100次这样完整的变化后,点B到达的位置坐标为( )
 正方形ABCD在坐标系中的位置如图所示,将正方形ABCD沿x轴翻折一次,再沿轴翻折一次,然后向右平移1个单位记作:图形的一次完整变化,图形经历100次这样完整的变化后,点B到达的位置坐标为( )
正方形ABCD在坐标系中的位置如图所示,将正方形ABCD沿x轴翻折一次,再沿轴翻折一次,然后向右平移1个单位记作:图形的一次完整变化,图形经历100次这样完整的变化后,点B到达的位置坐标为( )| A. | (-1,-4) | B. | (2,4) | C. | (-1,-4) | D. | (1,4) |
9. 如图,AB、AC是⊙O的两条弦,连结OB、OC.若∠BAC=60°,则∠BOC的度数( )
如图,AB、AC是⊙O的两条弦,连结OB、OC.若∠BAC=60°,则∠BOC的度数( )
 如图,AB、AC是⊙O的两条弦,连结OB、OC.若∠BAC=60°,则∠BOC的度数( )
如图,AB、AC是⊙O的两条弦,连结OB、OC.若∠BAC=60°,则∠BOC的度数( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
 已知,如图,在△ABC中,点D,E分别在AB和BC上,DE的延长线交AC的延长线于点F,且BD=CF,DE=EF.
已知,如图,在△ABC中,点D,E分别在AB和BC上,DE的延长线交AC的延长线于点F,且BD=CF,DE=EF.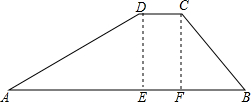 如图,水库大坝的横截面是梯形,坝顶CD宽是5m,坝高DE为20m,斜坡AD的坡度为1:$\sqrt{3}$,斜坡CB的坡度为5:6,建造这样的大坝1000m需要多少m3的土?(结果保留根号)
如图,水库大坝的横截面是梯形,坝顶CD宽是5m,坝高DE为20m,斜坡AD的坡度为1:$\sqrt{3}$,斜坡CB的坡度为5:6,建造这样的大坝1000m需要多少m3的土?(结果保留根号) 在平行四边形ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF、BF.
在平行四边形ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF、BF.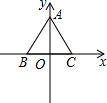 如图,等腰三角形ABC的腰长为5,底边BC=6,以BC所在的直线为x轴,BC的垂直平分线为y轴建立如图所示的直角坐标系,则点A的坐标为(0,4).
如图,等腰三角形ABC的腰长为5,底边BC=6,以BC所在的直线为x轴,BC的垂直平分线为y轴建立如图所示的直角坐标系,则点A的坐标为(0,4).