题目内容
19.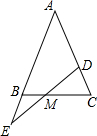 在等腰三角形ABC的腰AC上取一点D,腰AB的延长线上取一点E,使CD=BE,交BC于M,探索能得到的结论,并证明.
在等腰三角形ABC的腰AC上取一点D,腰AB的延长线上取一点E,使CD=BE,交BC于M,探索能得到的结论,并证明.解:结论是DM=EM.
证明:
分析 结论为DM=EM,理由为:过D作DF平行于AE,利用两直线平行同位角相等,内错角相等得到两对角相等,由AB=AC,利用等边对等角得到∠ABC=∠C,等量代换及等角对等边得到DC=DF,由DC=BE,等量代换得到DF=EB,利用AAS得到三角形DFM与三角形EBM全等,利用全等三角形对应边相等即可得证.
解答 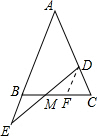 解:结论是DM=EM,
解:结论是DM=EM,
证明:过D作DF∥AE,
∴∠DFC=∠ABC,∠DFM=∠EBM,
∵AB=AC,
∴∠ABC=∠C,
∴∠DFC=∠C,
∴DC=DF,
∵DC=BE,
∴DF=BE,
在△DFM和△EBM中,
$\left\{\begin{array}{l}{∠DFM=∠EBM}\\{∠DMF=∠EMB}\\{DF=BE}\end{array}\right.$,
∴△DFM≌△EBM(AAS),
∴DM=EM.
故答案为:DM=EM.
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
16. 在平行四边形ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF、BF.
在平行四边形ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF、BF.
(1)求证:四边形BFDE是矩形.
(2)若CF=3,BF=4,DF=5,求证:△ADF是等腰三角形.
 在平行四边形ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF、BF.
在平行四边形ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF、BF.(1)求证:四边形BFDE是矩形.
(2)若CF=3,BF=4,DF=5,求证:△ADF是等腰三角形.
8.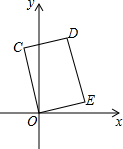 如图,在矩形COED中,点D的坐标是(1,3),则CE的长是( )
如图,在矩形COED中,点D的坐标是(1,3),则CE的长是( )
 如图,在矩形COED中,点D的坐标是(1,3),则CE的长是( )
如图,在矩形COED中,点D的坐标是(1,3),则CE的长是( )| A. | 3 | B. | $2\sqrt{2}$ | C. | $\sqrt{10}$ | D. | 4 |
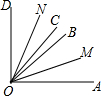 如图OM平分∠AOB,ON平分∠COD,若∠MON=50°,∠BOC=10°,求∠AOD的度数.
如图OM平分∠AOB,ON平分∠COD,若∠MON=50°,∠BOC=10°,求∠AOD的度数.
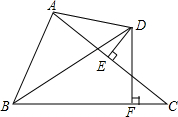 如图,△ABC中,AC的垂直平分线DE交AC于E,交∠ABC的平分线于D,DF⊥BC于F
如图,△ABC中,AC的垂直平分线DE交AC于E,交∠ABC的平分线于D,DF⊥BC于F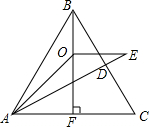 如图,在等边△ABC中,D是BC上任一点,延长AD至E,使AE=AB,作∠BAE的平分线交△ABC的高BF于O点,求∠AEO的度数.
如图,在等边△ABC中,D是BC上任一点,延长AD至E,使AE=AB,作∠BAE的平分线交△ABC的高BF于O点,求∠AEO的度数.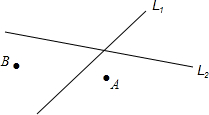 如图,直线L1、L2表示两条相交的公路,点A,B表示两个小镇,现在要在它们附近建一个加油站,使加油站到两条公路的距离相等,并到两个小镇的距离也相等,加油站应建在何处?请你在图上标出加油站的位置.(用尺规作图,并保留作图痕迹)
如图,直线L1、L2表示两条相交的公路,点A,B表示两个小镇,现在要在它们附近建一个加油站,使加油站到两条公路的距离相等,并到两个小镇的距离也相等,加油站应建在何处?请你在图上标出加油站的位置.(用尺规作图,并保留作图痕迹)