题目内容
阅读理解:对于二次三项式x2+2ax+a2可以直接用公式法分解为(x+a)2的形式,但对于二次三项式x2+2ax-8a2,就不能直接用公式法了,我们可以在二次三项式x2+2ax-8a2中先加上一项a2,使其成为完全
平方式,再减去a2这项,使整个式子的值不变.于是有:x2+2ax-8a2
=x2+2ax-8a2+a2-a2
=(x2+2ax+a2)-8a2-a2
=(x+a)2-9a2
=[(x+a)+3a][(x+a)-3a]
=((x+4a)(x-2a)像这样把二次三项式分解因式的方法叫做添(拆)项法.
(1)请认真阅读以上的添(拆)项法,并用上述方法将二次三项式:x2+2ax-3a2分解因式
(2)直接填空:请用上述的添 项法将方程的x2-4xy+3y2=0化为(x )•(x )=0
并直接写出y与x的关系式.(满足xy≠0,且x≠y)
(3)先化简
-
-
,再利用(2)中y与x的关系式求值.
平方式,再减去a2这项,使整个式子的值不变.于是有:x2+2ax-8a2
=x2+2ax-8a2+a2-a2
=(x2+2ax+a2)-8a2-a2
=(x+a)2-9a2
=[(x+a)+3a][(x+a)-3a]
=((x+4a)(x-2a)像这样把二次三项式分解因式的方法叫做添(拆)项法.
(1)请认真阅读以上的添(拆)项法,并用上述方法将二次三项式:x2+2ax-3a2分解因式
(2)直接填空:请用上述的添
并直接写出y与x的关系式.(满足xy≠0,且x≠y)
(3)先化简
| x |
| y |
| y |
| x |
| x2+y2 |
| xy |
考点:因式分解的应用
专题:
分析:(1)把-3a2拆成a2-a2-3a2,进一步利用完全平方公式和平方差公式因式分解即可;
(2)类比(1)的方法得出答案即可;
(3)先通分,再进一步化简,再代入(2)中y与x的关系式求得数值即可.
(2)类比(1)的方法得出答案即可;
(3)先通分,再进一步化简,再代入(2)中y与x的关系式求得数值即可.
解答:解:(1)x2+2ax-3a2
=x2+2ax+a2-a2-3a2
=(x+a)2-(2a)2
=(x+a+2a)(x+a-2a)
=(x+3a)(x-a);
(2)x2-4xy+3y2=0
可化为(x-y)(x-3y)=0,
可得 x-y=0或x-3y=0
x=y或x=3y
∵x≠y或xy≠0
∴x=3y;
(3)原式=
=
=-
把x=3y代入①式中
原式=-
=-
.
=x2+2ax+a2-a2-3a2
=(x+a)2-(2a)2
=(x+a+2a)(x+a-2a)
=(x+3a)(x-a);
(2)x2-4xy+3y2=0
可化为(x-y)(x-3y)=0,
可得 x-y=0或x-3y=0
x=y或x=3y
∵x≠y或xy≠0
∴x=3y;
(3)原式=
| x2-y2-(x2+y2) |
| xy |
=
| -2y2 |
| xy |
=-
| 2y |
| x |
把x=3y代入①式中
原式=-
| 2y |
| 3y |
=-
| 2 |
| 3 |
点评:此题考查因式分解的运用,注意式子的特点,灵活添加某一项,进一步利用公式法因式分解即可.

练习册系列答案
相关题目
 如图是2011年末杭州市八个区的人口统计图,则下列说法中错误的是( )
如图是2011年末杭州市八个区的人口统计图,则下列说法中错误的是( )| A、人数最多的区比最少的区多不到50万人 |
| B、江干区比西湖区多20万人口 |
| C、有1个区的人口数不到50万 |
| D、人口超过100万的区有2个 |
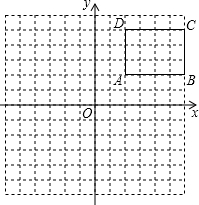 作图题:如图,在平面直角坐标系中,矩形ABCD的各顶点的坐标分别为A(2,2),B(6,2),C(6,5),D(2,5).
作图题:如图,在平面直角坐标系中,矩形ABCD的各顶点的坐标分别为A(2,2),B(6,2),C(6,5),D(2,5).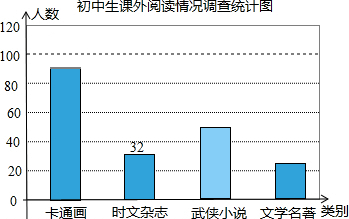 4月23日是“世界读书日”,今年世界读书日的主题是“阅读,让我们的世界更丰富”.某校随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图.请根据统计图表提供的信息解答下列问题:
4月23日是“世界读书日”,今年世界读书日的主题是“阅读,让我们的世界更丰富”.某校随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图.请根据统计图表提供的信息解答下列问题: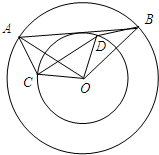 如图,两个同心圆的圆心为O,两圆的半径分别为5,3,其中A,B两点在大圆上,C,D在小圆上,且∠AOB=∠COD.
如图,两个同心圆的圆心为O,两圆的半径分别为5,3,其中A,B两点在大圆上,C,D在小圆上,且∠AOB=∠COD. 如图,已知△ABC中,以AB为直径的半⊙O交AC于D,交BC于E,BE=CE,∠C=70°,求∠DOE的度数.
如图,已知△ABC中,以AB为直径的半⊙O交AC于D,交BC于E,BE=CE,∠C=70°,求∠DOE的度数.

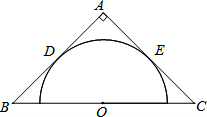 如图,在等腰直角三角形ABC中,AB=AC=8,O为BC的中点,以O为圆心作半圆,使它与AB,AC都相切,切点分别为D,E,则⊙O的半径为
如图,在等腰直角三角形ABC中,AB=AC=8,O为BC的中点,以O为圆心作半圆,使它与AB,AC都相切,切点分别为D,E,则⊙O的半径为