题目内容
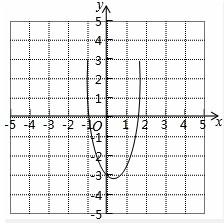
 在平面直角坐标系xOy中,二次函数y=2x2+bx+c的图象经过(-1,0)和(
在平面直角坐标系xOy中,二次函数y=2x2+bx+c的图象经过(-1,0)和(| 3 |
| 2 |
(1)求此二次函数的表达式.
(2)直接写出当-
| 3 |
| 2 |
(3)将一次函数 y=(1-m)x+2的图象向下平移m个单位后,与二次函数y=2x2+bx+c图象交点的横坐标分别是a和b,其中a<2<b,试求m的取值范围.
考点:待定系数法求二次函数解析式,二次函数图象与几何变换,二次函数与不等式(组)
专题:
分析:(1)由二次函数的图象经过(-1,0)和(
,0)两点,组成方程组再解即可求得二次函数的表达式;
(2)根据图象即可得出当-
<x<1时,y的取值范围;
(3)将一次函数 y=(1-m)x+2的图象向下平移m个单位后的一次函数表达式为y=(1-m)x+2-m,由题意得2x2-x-3=(1-m)x+2-m,整理得2x2+(m-2)x+m-5=0,因为a<2<b,a≠b,△=(m-2)2-4×2×(m-5)=(m-6)2+8>0,把x=2代入(1-m)x+2-m>2x2-x-3,解得m<
,所以m的取值范围为m<
的全体实数.
| 3 |
| 2 |
(2)根据图象即可得出当-
| 3 |
| 2 |
(3)将一次函数 y=(1-m)x+2的图象向下平移m个单位后的一次函数表达式为y=(1-m)x+2-m,由题意得2x2-x-3=(1-m)x+2-m,整理得2x2+(m-2)x+m-5=0,因为a<2<b,a≠b,△=(m-2)2-4×2×(m-5)=(m-6)2+8>0,把x=2代入(1-m)x+2-m>2x2-x-3,解得m<
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:(1)由二次函数的图象经过(-1,0)和(
,0)两点.
解得
∴此二次函数的表达式y=2x2-x-3;
(2)当x=-
时,y=3,当x=1时,y=-2,
又∵二次函数的顶点坐标是(
,-
)
∴当-
<x<1时,y的取值范围是-
<y<3;
(3)将一次函数 y=(1-m)x+2的图象向下平移m个单位后的一次函数表达式为y=(1-m)x+2-m,
∵y=(1-m)x+2-m与二次函数y=2x2+bx+c图象交点的横坐标为a和b,
∴2x2-x-3=(1-m)x+2-m,整理得
2x2+(m-2)x+m-5=0
∵a<2<b
∴a≠b
∴△=(m-2)2-4×2×(m-5)=(m-6)2+8>0
∴m≠1
∵a<2<b
当x=2时,(1-m)x+2-m>2x2-x-3
把x=2代入(1-m)x+2-m>2x2-x-3,解得m<
∴m的取值范围为m<
的全体实数.
| 3 |
| 2 |

|
解得
|
∴此二次函数的表达式y=2x2-x-3;
(2)当x=-
| 3 |
| 2 |
又∵二次函数的顶点坐标是(
| 1 |
| 4 |
| 25 |
| 8 |
∴当-
| 3 |
| 2 |
| 25 |
| 8 |
(3)将一次函数 y=(1-m)x+2的图象向下平移m个单位后的一次函数表达式为y=(1-m)x+2-m,
∵y=(1-m)x+2-m与二次函数y=2x2+bx+c图象交点的横坐标为a和b,
∴2x2-x-3=(1-m)x+2-m,整理得
2x2+(m-2)x+m-5=0
∵a<2<b
∴a≠b
∴△=(m-2)2-4×2×(m-5)=(m-6)2+8>0
∴m≠1
∵a<2<b
当x=2时,(1-m)x+2-m>2x2-x-3
把x=2代入(1-m)x+2-m>2x2-x-3,解得m<
| 1 |
| 3 |
∴m的取值范围为m<
| 1 |
| 3 |
点评:本题主要考查了求二次函数的解析式以及二次函数的图象与几何变换.

练习册系列答案
相关题目
抛物线y=x2-2x与坐标轴交点为( )
| A、二个交点 | B、一个交点 |
| C、无交点 | D、三个交点 |
 四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.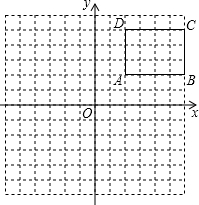 作图题:如图,在平面直角坐标系中,矩形ABCD的各顶点的坐标分别为A(2,2),B(6,2),C(6,5),D(2,5).
作图题:如图,在平面直角坐标系中,矩形ABCD的各顶点的坐标分别为A(2,2),B(6,2),C(6,5),D(2,5).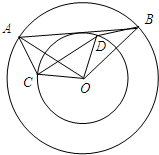 如图,两个同心圆的圆心为O,两圆的半径分别为5,3,其中A,B两点在大圆上,C,D在小圆上,且∠AOB=∠COD.
如图,两个同心圆的圆心为O,两圆的半径分别为5,3,其中A,B两点在大圆上,C,D在小圆上,且∠AOB=∠COD. 如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路.现新修一条路AC到公路l.小明测量出∠ACD=31°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度?(精确到0.1m;参考数据 tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).
如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路.现新修一条路AC到公路l.小明测量出∠ACD=31°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度?(精确到0.1m;参考数据 tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).