题目内容
对于正数x,规定f(x)=
,例如f(3)=
=
,f(
)=
=
,计算f(
)+f(
)+f(
)+…+f(
)+f(
)+f(1)+f(2)+f(3)+…+f(2012)+f(2013)+f(2014)的结果是( )
| x |
| 1+x |
| 3 |
| 1+3 |
| 3 |
| 4 |
| 1 |
| 3 |
| ||
1+
|
| 1 |
| 4 |
| 1 |
| 2014 |
| 1 |
| 2013 |
| 1 |
| 2012 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、2013 |
| B、2013.5 |
| C、2014 |
| D、2014.5 |
考点:分式的加减法
专题:新定义
分析:根据题意得到f(x)+f(
)=1,且f(1)=
,原式结合后利用此结论变形,计算即可得到结果.
| 1 |
| x |
| 1 |
| 2 |
解答:解:根据题意得:f(x)+f(
)=
+
=
=1,f(1)=
,
则原式=[f(
)+f(2014)]+[f(
)+f(2013)]+…+[f(
)+f(2)]+f(1)
=1+1+…+1+
=2013.5.
故选B.
| 1 |
| x |
| x |
| 1+x |
| ||
1+
|
| x+1 |
| x+1 |
| 1 |
| 2 |
则原式=[f(
| 1 |
| 2014 |
| 1 |
| 2013 |
| 1 |
| 2 |
=1+1+…+1+
| 1 |
| 2 |
=2013.5.
故选B.
点评:此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
若x=5是分式方程
-
=0的根,则( )
| a |
| x-2 |
| 15 |
| x |
| A、a=-5 | B、a=5 |
| C、a=-9 | D、a=9 |
抛物线y=x2-2x与坐标轴交点为( )
| A、二个交点 | B、一个交点 |
| C、无交点 | D、三个交点 |
投掷2个骰子,得到的两个点数都是质数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在Rt△ABC中,∠C=90°,sinA=
,AB=5,则边AC的长是( )
| 3 |
| 4 |
| A、3 | ||||
B、
| ||||
C、
| ||||
| D、4 |
 如图是2011年末杭州市八个区的人口统计图,则下列说法中错误的是( )
如图是2011年末杭州市八个区的人口统计图,则下列说法中错误的是( )| A、人数最多的区比最少的区多不到50万人 |
| B、江干区比西湖区多20万人口 |
| C、有1个区的人口数不到50万 |
| D、人口超过100万的区有2个 |
 四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.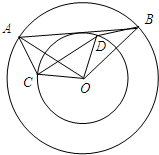 如图,两个同心圆的圆心为O,两圆的半径分别为5,3,其中A,B两点在大圆上,C,D在小圆上,且∠AOB=∠COD.
如图,两个同心圆的圆心为O,两圆的半径分别为5,3,其中A,B两点在大圆上,C,D在小圆上,且∠AOB=∠COD.