题目内容
已知方程x2-5x+a+3=0有两个正整数根,则a的值是( )
| A、a=1 |
| B、a=3 |
| C、a=1或a=3 |
| D、a=1或a=4 |
考点:一元二次方程的整数根与有理根
专题:计算题
分析:方程有两个正整数根,说明根的判别式△≥0,即25-4(a+3)≥0,由此可以求出a的取值范围,然后根据方程有两个正整数根确定a的值.
解答:解:∵x2-5x+a+3=0有两个正整数根,
∴△=25-4(a+3)≥0,
解得:a≤
,
∵方程的根是x=-
,
又因为是两个正整数根,
则25-4(a+3)=13-4a为完全平方数,
则a可取1、3,
当a=1时,方程的根为1和4;
当a=3时,方程的根为3和1;
综上可得a=1、3均符合题意.
故选:C.
∴△=25-4(a+3)≥0,
解得:a≤
| 13 |
| 4 |
∵方程的根是x=-
5±
| ||
| 2 |
又因为是两个正整数根,
则25-4(a+3)=13-4a为完全平方数,
则a可取1、3,
当a=1时,方程的根为1和4;
当a=3时,方程的根为3和1;
综上可得a=1、3均符合题意.
故选:C.
点评:此题主要考查了一元二次方程的整数根和有理根的知识,要求我们熟练:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根,正确确定a的范围,并进行正确的检验是解决本题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
 甲、乙、丙三个组生产帐蓬支援灾区,已知女工人3人每天共生产4顶帐蓬,男工人2人每天共生产3顶帐蓬.下图是描述三个组一天生产帐蓬情况的统计图,从中可得出人数最多的组是
甲、乙、丙三个组生产帐蓬支援灾区,已知女工人3人每天共生产4顶帐蓬,男工人2人每天共生产3顶帐蓬.下图是描述三个组一天生产帐蓬情况的统计图,从中可得出人数最多的组是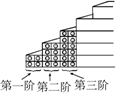 如图,有一楼梯每一阶的长度、宽度与增加的高度都一样.有一工人在此楼梯的一侧贴上大小相同的正方形磁砖,第一阶贴了4块,第二阶贴了8块,…,依此规律共贴了144块磁砖后,刚好贴完楼梯的一侧.则此楼梯共有
如图,有一楼梯每一阶的长度、宽度与增加的高度都一样.有一工人在此楼梯的一侧贴上大小相同的正方形磁砖,第一阶贴了4块,第二阶贴了8块,…,依此规律共贴了144块磁砖后,刚好贴完楼梯的一侧.则此楼梯共有