题目内容
在平面直角坐标系中,点A和点B分别在x轴的负半轴和y轴的正半轴上,且OA、OB分别是关于x的方程x2-7x+12=0的两个根(OA<OB)
(1)求直线AB的解析式;
(2)线段AB上一点C使得S△ACO:S△BCO=1:2,请求出点C的坐标;
(3)在(2)的条件下,y轴上是否存在一点D,使得以点A、C、O、D为顶点的四边形是梯形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
(1)求直线AB的解析式;
(2)线段AB上一点C使得S△ACO:S△BCO=1:2,请求出点C的坐标;
(3)在(2)的条件下,y轴上是否存在一点D,使得以点A、C、O、D为顶点的四边形是梯形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
考点:一次函数综合题,解二元一次方程组,待定系数法求一次函数解析式,梯形,平行线分线段成比例
专题:计算题
分析:(1)求出一元二次方程的解,得出OA、OB的值,求出A、B的坐标,设直线AB的解析式是:y=kx+b,把A(-3,0)、B(0,4)代入得出方程组,求出方程组的解即可;
(2)根据△ACO边AC上的高和△BCO边BC上的高相等和已知求出
=
,C作CE⊥y轴于E,CF⊥x轴于F,根据平行线分线段成比例定理求出CE、CF的值,即可得出C的坐标;
(3)分为两种情况:①当CD∥OA,即D在E处时,根据E的坐标即可求出的坐标;②当D在y轴的负半轴上D′处时,得出
=
,求出OD的值,即可得出D的坐标.
(2)根据△ACO边AC上的高和△BCO边BC上的高相等和已知求出
| BC |
| AC |
| 2 |
| 1 |
(3)分为两种情况:①当CD∥OA,即D在E处时,根据E的坐标即可求出的坐标;②当D在y轴的负半轴上D′处时,得出
| BC |
| AC |
| BO |
| OD |
解答:(1)解:x2-7x+12=0,
x1=3,x2=4,
∵OA<OB,
∴OA=3,OB=4,
∴A(-3,0),B(0,4),
设直线AB的解析式是:y=kx+b,
把A(-3,0)、B(0,4)代入得:
,
解得:
,
∴直线AB的解析式是y=
x+4.
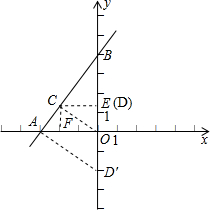
(2)解:∵△ACO边AC上的高和△BCO边BC上的高相等,
∵S△ACO:S△BCO=1:2,
∴
=
,
过C作CE⊥y轴于E,CF⊥x轴于F,
∴CE∥x轴,CF∥y轴,
∴
=
=
,
∵OA=3,
∴CE=2,
同理CF=
,
∴点C的坐标是(-2,
).
(3)解:存在,
理由是:∵AC和DO相交,
分为两种情况:①如图所示:当CD∥OA,即D在E处时,四边形AODC是梯形,
D的坐标是(0,
);
②如图所示:当D在y轴的负半轴上D′处时,OC∥AD,
∴
=
,
即
=
,
∴OD=2,
D的坐标是(0,-2),
答:在(2)的条件下,y轴上存在一点D,使得以点A、C、O、D为顶点的四边形是梯形,点D的坐标是(0,
)或(0,-2).
x1=3,x2=4,
∵OA<OB,
∴OA=3,OB=4,
∴A(-3,0),B(0,4),
设直线AB的解析式是:y=kx+b,
把A(-3,0)、B(0,4)代入得:
|
解得:
|
∴直线AB的解析式是y=
| 4 |
| 3 |
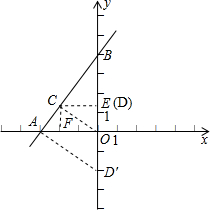
(2)解:∵△ACO边AC上的高和△BCO边BC上的高相等,
∵S△ACO:S△BCO=1:2,
∴
| AC |
| BC |
| 1 |
| 2 |
过C作CE⊥y轴于E,CF⊥x轴于F,
∴CE∥x轴,CF∥y轴,
∴
| CE |
| OA |
| BC |
| AB |
| 2 |
| 2+1 |
∵OA=3,
∴CE=2,
同理CF=
| 4 |
| 3 |
∴点C的坐标是(-2,
| 4 |
| 3 |
(3)解:存在,
理由是:∵AC和DO相交,
分为两种情况:①如图所示:当CD∥OA,即D在E处时,四边形AODC是梯形,
D的坐标是(0,
| 4 |
| 3 |
②如图所示:当D在y轴的负半轴上D′处时,OC∥AD,
∴
| BC |
| AC |
| BO |
| OD |
即
| 2 |
| 1 |
| 4 |
| OD |
∴OD=2,
D的坐标是(0,-2),
答:在(2)的条件下,y轴上存在一点D,使得以点A、C、O、D为顶点的四边形是梯形,点D的坐标是(0,
| 4 |
| 3 |
点评:本题考查了梯形、平行线分线段成比例定理,用待定系数法求一次函数的解析式,解二元一次方程组等知识点的应用,主要培养学生的推理能力和计算能力,题目综合性比较强,是一道具有代表性的题目,分类讨论思想的灵活运用.

练习册系列答案
相关题目
 伸出一只手,从大拇指开始按如图所示的那样数数字:1,2,3,4,…,则2004落在( )
伸出一只手,从大拇指开始按如图所示的那样数数字:1,2,3,4,…,则2004落在( )| A、大拇指上 | B、食指上 |
| C、中指上 | D、无名指上 |
已知方程x2-5x+a+3=0有两个正整数根,则a的值是( )
| A、a=1 |
| B、a=3 |
| C、a=1或a=3 |
| D、a=1或a=4 |
 已知图中三十六个小等边三角形的面积都等于1,则三角形ABC的面积为( )
已知图中三十六个小等边三角形的面积都等于1,则三角形ABC的面积为( )| A、21 | B、22 | C、23 | D、24 |
下列多边形中,既是轴对称图形又是中心对称图形的是( )
| A、平行四边形 | B、等腰梯形 |
| C、圆 | D、等边三角形 |