题目内容
14.下列根式$\sqrt{\frac{1}{3}}$、$\sqrt{18}$、$\sqrt{24}$、$\sqrt{\frac{3}{2}}$中,与$\sqrt{3}$是同类二次根式的是$\sqrt{\frac{1}{3}}$.分析 首先把每个根式进行化简,根据同类二次根式的定义即可作出判断.
解答 解:$\sqrt{\frac{1}{3}}$=$\frac{1}{3}$$\sqrt{3}$、$\sqrt{18}$=3$\sqrt{2}$、$\sqrt{24}$=2$\sqrt{6}$、$\sqrt{\frac{3}{2}}$=$\frac{1}{2}$$\sqrt{6}$,
故与$\sqrt{3}$是同类二次根式的是$\sqrt{\frac{1}{3}}$.
故答案为:$\sqrt{\frac{1}{3}}$.
点评 本题考查同类二次根式的概念,同类二次根式是化为最简二次根式后,被开方数相同的二次根式称为同类二次根式.

练习册系列答案
相关题目
9.下列说法中错误的是( )
| A. | 原点的坐标是(0,0) | |
| B. | x轴上所有点的纵坐标相等 | |
| C. | 与y轴平行的直线上所有点的横坐标相等 | |
| D. | 点(0,-1)在第四象限 |
19.已知m,n分别是一个三角形的底和该底上的高,且满足(m-n)2=5,(m+n)2=11,则此三角形的面积为( )
| A. | 24 | B. | 12 | C. | $\frac{3}{2}$ | D. | $\frac{3}{4}$ |
6.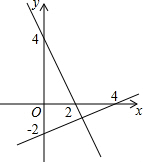 两个一次函数的图象如图所示,下列方程组的解满足交点P的坐标的是( )
两个一次函数的图象如图所示,下列方程组的解满足交点P的坐标的是( )
 两个一次函数的图象如图所示,下列方程组的解满足交点P的坐标的是( )
两个一次函数的图象如图所示,下列方程组的解满足交点P的坐标的是( )| A. | $\left\{\begin{array}{l}{x-2y=4}\\{2x-y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+2y=4}\\{2x-y=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+2y=4}\\{2x+y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-2y=4}\\{2x+y=4}\end{array}\right.$ |
4.下列运算正确的是( )
| A. | (2a2)2=2a4 | B. | 6a8÷3a2=2a4 | C. | 2a2•a=2a3 | D. | 3a2-2a2=1 |






