题目内容
6.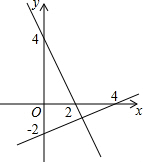 两个一次函数的图象如图所示,下列方程组的解满足交点P的坐标的是( )
两个一次函数的图象如图所示,下列方程组的解满足交点P的坐标的是( )| A. | $\left\{\begin{array}{l}{x-2y=4}\\{2x-y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+2y=4}\\{2x-y=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+2y=4}\\{2x+y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-2y=4}\\{2x+y=4}\end{array}\right.$ |
分析 先利用待定系数法求出两直线的解析式,然后根据方程组的解就是两个相应的一次函数图象的交点坐标,把两个解析式组成方程组即可.
解答 解:过点(0,4),(2,0)的直线解析式为y=-2x+4,
过点(0,-2),(4,0)的直线解析式为y=$\frac{1}{2}$x-4,
所以方程组$\left\{\begin{array}{l}{y=-2x+4}\\{y=\frac{1}{2}x-2}\end{array}\right.$的解满足交点P的坐标.
故选D.
点评 本题考查了一次函数与二元一次方程(组):方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的一次函数式,因此方程组的解就是两个相应的一次函数图象的交点坐标.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.下列计算中:①$\sqrt{2}+\sqrt{3}$=$\sqrt{5}$,②2+$\sqrt{2}$=2$\sqrt{2}$;③3$\sqrt{2}$-$\sqrt{2}$=3;④3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$,正确的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
11.下列图示中,直线表示方法正确的有( )

| A. | ①②③④ | B. | ①② | C. | ②④ | D. | ①④ |
15.若关于x的一元二次方程(k-1)x2+4x+1=0有实数根,则k的取值范围是( )
| A. | k≤5 | B. | k≤5,且k≠1 | C. | k<5,且k≠1 | D. | k<5 |
7.小慧在解方程2a-2x=5(x为未知数)时,误将“-2x”写成了“+2x”,得到方程的解为x=-5,则原方程的解为( )
| A. | x=-3 | B. | x=3 | C. | x=5 | D. | x=-5 |

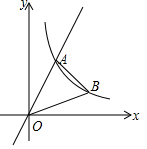 如图,直线y=3x与双曲线y=$\frac{k}{x}$(k≠0,且x>0)交于点A,点A的横坐标是1.
如图,直线y=3x与双曲线y=$\frac{k}{x}$(k≠0,且x>0)交于点A,点A的横坐标是1.