题目内容
在Rt△ABC中,AB=BC,E为BC中点,点D在射线BA上,连接DE,过点B作BM⊥DE于M,过点A作AN⊥DE于N.当点D是边AB的中点时如图1,易证:AN+BM=2EM.
当点D的位置如图2和图3时,上述结论是否成立,若成立,请给与证明;若不成立,线段AN、BM、EM之间又有怎样的相等关系.写出你的猜想,不必证明.
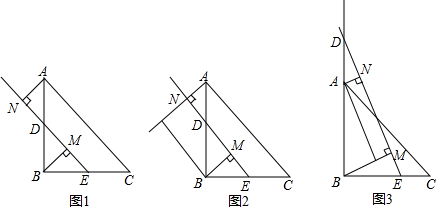
当点D的位置如图2和图3时,上述结论是否成立,若成立,请给与证明;若不成立,线段AN、BM、EM之间又有怎样的相等关系.写出你的猜想,不必证明.

考点:全等三角形的判定与性质
专题:
分析:(1)当点D在线段AB上,易证四边形BGNM为矩形,可得GN=BM,即可求得AN+BM=AG,易证△AGB∽△EMB,可得
=
=2,即可解题;
(2)当点D在BA延长线上时,AN+BM=2EM不成立,新结论为BM-AN=2EM,理由:易证四边形AGMN是矩形,可得GM=AN,即可求得BG=BM-AN,易证△AGB∽△BME,可得
=
=2,即可解题.
| AG |
| EM |
| AB |
| BE |
(2)当点D在BA延长线上时,AN+BM=2EM不成立,新结论为BM-AN=2EM,理由:易证四边形AGMN是矩形,可得GM=AN,即可求得BG=BM-AN,易证△AGB∽△BME,可得
| BG |
| EM |
| AB |
| BE |
解答:证明:(1)如图2,当点D在线段AB上,
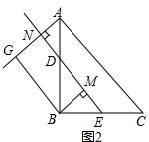
∵∠BMN=∠MNG=∠NGB=90°,
∴四边形BGNM为矩形,
∴GN=BM,
∴AN+BM=AG,
∵∠ABG+∠ABM=90°,∠ABM+∠MBE=90°,
∴∠MBE=∠ABG,
∵∠AGB=∠BME=90°,
∴△AGB∽△EMB,
∴
=
=2,
∴AN+BM=AG=2EM;
(2)如图3,当点D在BA延长线上时,AN+BM=2EM不成立,新结论为BM-AN=2EM,
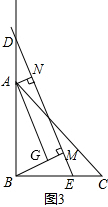
理由:∵∠ANM=∠BMN=∠AGM=90°,
∴四边形AGMN是矩形,
∴GM=AN,
∴BG=BM-GM=BM-AN,
∵∠BAG+∠ABG=90°,∠ABG+∠EBM=90°,
∴∠EBM=∠BAG,
∵∠AGB=∠BME=90°,
∴△AGB∽△BME,
∴
=
=2,
∴BM-AN=BG=2EM.

∵∠BMN=∠MNG=∠NGB=90°,
∴四边形BGNM为矩形,
∴GN=BM,
∴AN+BM=AG,
∵∠ABG+∠ABM=90°,∠ABM+∠MBE=90°,
∴∠MBE=∠ABG,
∵∠AGB=∠BME=90°,
∴△AGB∽△EMB,
∴
| AG |
| EM |
| AB |
| BE |
∴AN+BM=AG=2EM;
(2)如图3,当点D在BA延长线上时,AN+BM=2EM不成立,新结论为BM-AN=2EM,

理由:∵∠ANM=∠BMN=∠AGM=90°,
∴四边形AGMN是矩形,
∴GM=AN,
∴BG=BM-GM=BM-AN,
∵∠BAG+∠ABG=90°,∠ABG+∠EBM=90°,
∴∠EBM=∠BAG,
∵∠AGB=∠BME=90°,
∴△AGB∽△BME,
∴
| BG |
| EM |
| AB |
| BE |
∴BM-AN=BG=2EM.
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质,本题中求证△AGB∽△BME是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 如图,在△ABC中,D点是AB的中点,AC=5cm,BC=8cm.
如图,在△ABC中,D点是AB的中点,AC=5cm,BC=8cm.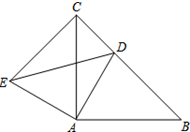 已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点.
已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点. 如图1,△ABC中,∠ACB=90°,CE⊥AB于E,D在线段AB上,AD=AC,AF平分∠CAE交CE于F.
如图1,△ABC中,∠ACB=90°,CE⊥AB于E,D在线段AB上,AD=AC,AF平分∠CAE交CE于F.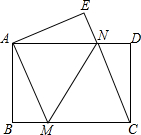 如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N. 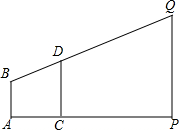 如图所示,旗杆顶部Q,标杆顶部D,观测者的眼睛B在同一直线上,测得观测者的脚到旗杆底部的距离AP=75m,观测者的脚到标杆底部的距离AC=2.5m,若AB=1.5m,标杆CD的高为2m,那么旗杆有多高.
如图所示,旗杆顶部Q,标杆顶部D,观测者的眼睛B在同一直线上,测得观测者的脚到旗杆底部的距离AP=75m,观测者的脚到标杆底部的距离AC=2.5m,若AB=1.5m,标杆CD的高为2m,那么旗杆有多高.