题目内容
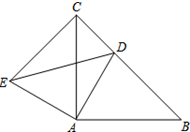 已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点.
已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点.(1)求证:△ACE≌△ABD;
(2)若AC=
| 8 |
考点:全等三角形的判定与性质,勾股定理,等腰直角三角形
专题:
分析:(1)易证∠EAC=∠DAB,即可证明△ACE≌△ABD;
(2)根据(1)中结论可得EC=BD,∠ACE=∠B=45°,即可求得∠ECD=90°,易求得BC得长,即可求得EC的长,在RT△ECD中,根据勾股定理即可求得DE的长,即可解题.
(2)根据(1)中结论可得EC=BD,∠ACE=∠B=45°,即可求得∠ECD=90°,易求得BC得长,即可求得EC的长,在RT△ECD中,根据勾股定理即可求得DE的长,即可解题.
解答:(1)证明:∵∠EAC+∠CAD=∠EAD=90°,∠CAD+∠DAB=∠BAC=90°,
∴∠EAC=∠DAB,
在△ACE和△ABD中,
,
∴△ACE≌△ABD(SAS);
(2)解:∵△ACE≌△ABD,
∴EC=BD,∠ACE=∠B=45°,
∴∠ECD=∠ACE+∠ACB=90°,
∵等腰直角△ABC中,AC=
,
∴BC=
AC=4,
∴EC=BD=BC-CD=3,
∴在RT△ECD中,DE=
=
.
∴∠EAC=∠DAB,
在△ACE和△ABD中,
|
∴△ACE≌△ABD(SAS);
(2)解:∵△ACE≌△ABD,
∴EC=BD,∠ACE=∠B=45°,
∴∠ECD=∠ACE+∠ACB=90°,
∵等腰直角△ABC中,AC=
| 8 |
∴BC=
| 2 |
∴EC=BD=BC-CD=3,
∴在RT△ECD中,DE=
| EC2+CD2 |
| 10 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了直角三角形中勾股定理的运用,本题中求证△ACE≌△ABD是解题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
 如图,在平面直角坐标系中,已知点A(2,0),以OA为边在第一象限内作等边三角形OAB,点P是x轴上一动点 (点P在点A的右侧),以线段BP为边作等边三角形BPQ.设点Q的坐标为(x,y),则y与x之间的关系式是
如图,在平面直角坐标系中,已知点A(2,0),以OA为边在第一象限内作等边三角形OAB,点P是x轴上一动点 (点P在点A的右侧),以线段BP为边作等边三角形BPQ.设点Q的坐标为(x,y),则y与x之间的关系式是 如图在Rt△ABC中,∠ACB=90°,AC=3,BC=4,则既平分△ABC周长又平分△ABC面积的直线有几条?
如图在Rt△ABC中,∠ACB=90°,AC=3,BC=4,则既平分△ABC周长又平分△ABC面积的直线有几条?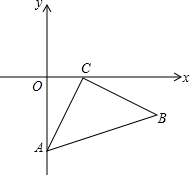 已知:在平面直角坐标系中,△ABC的顶点A(0,2),C(1,0)分别在y轴、x轴上,当点B在第四象限时,且∠ACB=90°,AC=BC.则点B的坐标为:(
已知:在平面直角坐标系中,△ABC的顶点A(0,2),C(1,0)分别在y轴、x轴上,当点B在第四象限时,且∠ACB=90°,AC=BC.则点B的坐标为:(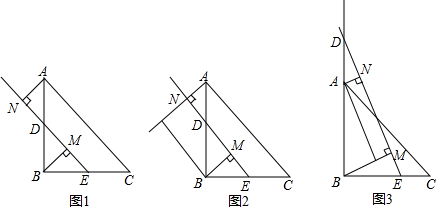
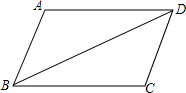 如图,已知:∠ABC=∠ADC,AD∥BC.请补充完整过程说明:AB=CD的理由.
如图,已知:∠ABC=∠ADC,AD∥BC.请补充完整过程说明:AB=CD的理由.