题目内容
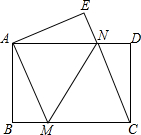 如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N. (1)求证:CM=CN;
(2)若△CMN的面积与△CDN的面积比为3:2,求
| MN |
| DN |
考点:翻折变换(折叠问题)
专题:
分析:(1)证明四边形AMCN是菱形,即可解决问题.
(2)根据题意求出
=
,设MC=3λ;用λ来表示CD、AB的长,运用面积公式即可解决问题.
(2)根据题意求出
| MC |
| DN |
| 3 |
| 2 |
解答: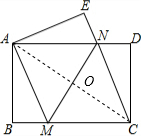 (1)证明:如图,连接AC交MN于点O;
(1)证明:如图,连接AC交MN于点O;
则MN⊥AC,且平分AC,
∴NA=NC;AO=CO;
∵矩形是中心对称图形,
∴MO=NO,而AO=CO,MN⊥AC,
∴四边形AMCN是菱形,
∴CM=CN.
(2)解:∵△CMN的面积与△CDN的面积比为3:2,
∴
=
,即
=
,
设MC=3λ,则DN=2λ,AD=5λ,CN=3λ;
由勾股定理得:CD2=CN2-DN2=5λ2,
∴CD=
λ;同理可求AC=
λ;
由面积公式得:MC•CD=
AC•MN,
即3λ•
λ=
×
λ•MN,
∴MN=
λ,
∴
=
.
 (1)证明:如图,连接AC交MN于点O;
(1)证明:如图,连接AC交MN于点O;则MN⊥AC,且平分AC,
∴NA=NC;AO=CO;
∵矩形是中心对称图形,
∴MO=NO,而AO=CO,MN⊥AC,
∴四边形AMCN是菱形,
∴CM=CN.
(2)解:∵△CMN的面积与△CDN的面积比为3:2,
∴
| ||
|
| 3 |
| 2 |
| MC |
| DN |
| 3 |
| 2 |
设MC=3λ,则DN=2λ,AD=5λ,CN=3λ;
由勾股定理得:CD2=CN2-DN2=5λ2,
∴CD=
| 5 |
| 30 |
由面积公式得:MC•CD=
| 1 |
| 2 |
即3λ•
| 5 |
| 1 |
| 2 |
| 30 |
∴MN=
| 6 |
∴
| MN |
| DN |
| ||
| 2 |
点评:该题主要考查了翻折变换及其应用问题;解题的关键是根据翻折变换的性质找出图形中隐含的等量关系,灵活运用勾股定理、菱形的判定等几何知识点来分析、判断、推理或解答;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
在Rt△ABC中,∠B=90°,AC=17cm,BC=8cm,则另一条直角边AB的长是( )
| A、13cm | B、14cm |
| C、15cm | D、16cm |
 如图,在平面直角坐标系中,已知点A(2,0),以OA为边在第一象限内作等边三角形OAB,点P是x轴上一动点 (点P在点A的右侧),以线段BP为边作等边三角形BPQ.设点Q的坐标为(x,y),则y与x之间的关系式是
如图,在平面直角坐标系中,已知点A(2,0),以OA为边在第一象限内作等边三角形OAB,点P是x轴上一动点 (点P在点A的右侧),以线段BP为边作等边三角形BPQ.设点Q的坐标为(x,y),则y与x之间的关系式是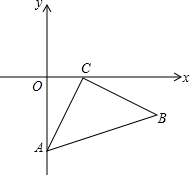 已知:在平面直角坐标系中,△ABC的顶点A(0,2),C(1,0)分别在y轴、x轴上,当点B在第四象限时,且∠ACB=90°,AC=BC.则点B的坐标为:(
已知:在平面直角坐标系中,△ABC的顶点A(0,2),C(1,0)分别在y轴、x轴上,当点B在第四象限时,且∠ACB=90°,AC=BC.则点B的坐标为:(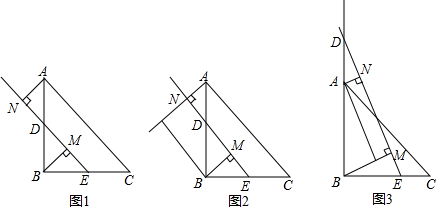
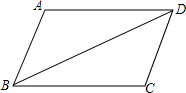 如图,已知:∠ABC=∠ADC,AD∥BC.请补充完整过程说明:AB=CD的理由.
如图,已知:∠ABC=∠ADC,AD∥BC.请补充完整过程说明:AB=CD的理由.