题目内容
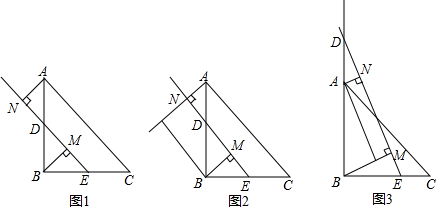
如图，在△ABC中，D点是AB的中点，AC=5cm，BC=8cm．（1）请你作出△CDB关于点D成中心对称的图形；
（2）你能求出CD的取值范围吗？
考点：作图-旋转变换
专题：
分析：（1）根据中心对称的性质，点B与点A关于点D对称，延长CD并使DE=CD，连接AE，△EAD即为所求图形；
（2）根据中心对称的性质可得AE=BC，然后利用三角形的任意两边之和大于第三边，三角形的任意两边之和大于第三边求出CE的取值范围，再求解即可．
（2）根据中心对称的性质可得AE=BC，然后利用三角形的任意两边之和大于第三边，三角形的任意两边之和大于第三边求出CE的取值范围，再求解即可．
解答：
解：（1）如图所示；
（2）∵△EAD与△CDB关于点D成中心对称，
∴AE=BC=8cm，
∵AC=5cm，
8-5=3cm，8+5=13cm，
∴3＜CE＜13，
∴1.5cm＜CD＜6.5cm．
解：（1）如图所示；（2）∵△EAD与△CDB关于点D成中心对称，
∴AE=BC=8cm，
∵AC=5cm，
8-5=3cm，8+5=13cm，
∴3＜CE＜13，
∴1.5cm＜CD＜6.5cm．
点评：本题考查了利用旋转变换作图，三角形的三边关系，熟记中心对称的性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
-1
的相反数是（ ）
| 1 |
| 4 |
A、1
| ||
B、-1
| ||
C、-
| ||
D、
|
如图，是一个数值转换机，根据所给的程序计算，若输入x的值为1，则输出y的值为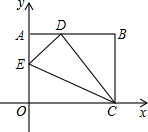
如图，将一矩形纸片OABC放在直角坐标系中，O为原点，C在x的正半轴上，OA=6，OC=10，在OA上取一点E，将△EOC沿EC折叠，使O点落在AB边上的D点，求E点的坐标．
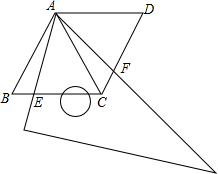用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD．把一个含60°角的三角尺与这个菱形叠合，如果使三角尺60°角的顶点与点A重合，两边分别与AB、AC重合，将三角尺绕A点按逆时针方向旋转．如图，三角尺的两边分别与菱形的两边BC、CD相交于点E、F．