题目内容
抽样统计甲、乙两位射击运动员的5次训练成绩(单位:环),结果如下:
则成绩较为稳定(方差较小)的那位运动员成绩的方差为 .
| 运动员 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 甲 | 87 | 91 | 90 | 89 | 93 |
| 乙 | 89 | 90 | 91 | 88 | 92 |
考点:方差
专题:
分析:直接由图表得出两组数据,求出它们的平均数,求出方差,则答案可求.
解答:解:由图表得到甲乙两位射击运动员的数据分别为:
甲:87,91,90,89,93;
乙:89,90,91,88,92;
甲的平均数=(87+91+90+89+93)÷5=90,
乙的平均数=(89+90+91+88+92)÷5=90,
则甲的方差=
[(87-90)2+(91-90)2+(90-90)2+(89-90)2+(93-90)2]=4,
乙的方差=
[(89-90)2+(90-90)2+(91-90)2+(88-90)2+(92-90)2]=2,
则乙运动员的成绩较稳定,方差为2.
故答案为:2.
甲:87,91,90,89,93;
乙:89,90,91,88,92;
甲的平均数=(87+91+90+89+93)÷5=90,
乙的平均数=(89+90+91+88+92)÷5=90,
则甲的方差=
| 1 |
| 5 |
乙的方差=
| 1 |
| 5 |
则乙运动员的成绩较稳定,方差为2.
故答案为:2.
点评:本题考查方差的定义:一般地设n个数据,x1,x2,…xn的平均数为
,则方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 某中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
某中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
 如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠P=60°,则∠AEB=
如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠P=60°,则∠AEB=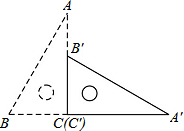 如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为
如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为 如图,每个小正方形边长为1,则△ABC边AC上的高BD的长为
如图,每个小正方形边长为1,则△ABC边AC上的高BD的长为