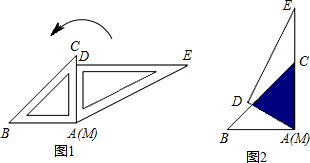题目内容
 如图,每个小正方形边长为1,则△ABC边AC上的高BD的长为
如图,每个小正方形边长为1,则△ABC边AC上的高BD的长为考点:勾股定理,三角形的面积
专题:网格型
分析:根据网格,利用勾股定理求出AC的长,AB的长,以及AB边上的高,利用三角形面积公式求出三角形ABC面积,而三角形ABC面积可以由AC与BD乘积的一半来求,利用面积法即可求出BD的长.
解答:解:根据勾股定理得:AC=
=5,
由网格得:S△ABC=
×2×4=4,且S△ABC=
AC•BD=
×5BD,
∴
×5BD=4,
解得:BD=
.
故答案为:
| 32+42 |
由网格得:S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
解得:BD=
| 8 |
| 5 |
故答案为:
| 8 |
| 5 |
点评:此题考查了勾股定理,以及三角形的面积,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
x3m+3可以写成( )
| A、3xm+1 |
| B、x3m+x3 |
| C、x3•xm+1 |
| D、x3m•x3 |
在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,以点C为圆心,5cm为半径的⊙C与边AB的位置关系是( )
| A、外离 | B、相切 | C、相交 | D、相离 |
 如图,菱形ABCD的周长
如图,菱形ABCD的周长 如图,∠ABC=45°,AC=5,H是高AD和BE的交点,则线段BH长为
如图,∠ABC=45°,AC=5,H是高AD和BE的交点,则线段BH长为 如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长
如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长