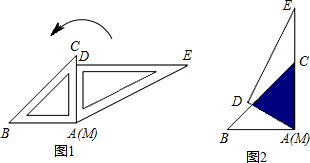题目内容
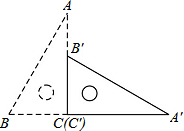 如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为
如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为考点:旋转的性质,平移的性质
专题:计算题
分析:作B′D⊥AB于D,如图,由∠A=30°得BC=
AB=6,AC=
BC=6
,再根据旋转的性质得B′C′=BC=6,则AB′=AC-B′C′=6
-6,
在Rt△ADB′中,根据含30度的直角三角形三边的关系得到DB′=
AB′=
×(6
-6)=6-2
,然后根据平移的性质得三角板A′B′C′平移的距离为(6-2
)cm.
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
在Rt△ADB′中,根据含30度的直角三角形三边的关系得到DB′=
| ||
| 3 |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
解答:解 :作B′D⊥AB于D,如图,
:作B′D⊥AB于D,如图,
∵AB=12,∠A=30°,
∴BC=
AB=6,
∴AC=
BC=6
,
∵三角板ABC绕C顺时针旋转90°至三角板A′B′C′的位置,
∴B′C′=BC=6,
∴AB′=AC-B′C′=6
-6,
在Rt△ADB′中,DB′=
AB′=
×(6
-6)=6-2
,
∴三角板A′B′C′平移的距离为(6-2
)cm.
故答案为(6-2
).
 :作B′D⊥AB于D,如图,
:作B′D⊥AB于D,如图,∵AB=12,∠A=30°,
∴BC=
| 1 |
| 2 |
∴AC=
| 3 |
| 3 |
∵三角板ABC绕C顺时针旋转90°至三角板A′B′C′的位置,
∴B′C′=BC=6,
∴AB′=AC-B′C′=6
| 3 |
在Rt△ADB′中,DB′=
| ||
| 3 |
| ||
| 3 |
| 3 |
| 3 |
∴三角板A′B′C′平移的距离为(6-2
| 3 |
故答案为(6-2
| 3 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了平移的性质和含30度的直角三角形三边的关系.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 如图,在一张长方形纸片ABCD中,AB=3
如图,在一张长方形纸片ABCD中,AB=3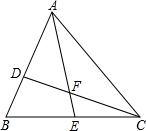 如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2,若S△ABC=12,则S1-S2的值为
如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2,若S△ABC=12,则S1-S2的值为