题目内容
11．某气象台发现：在某段时间里，如果早晨下雨，那么晚上是晴天；如果晚上下雨，那么早晨是晴天，已知这段时间有9天下了雨，并且有6天晚上是晴天，7天早晨是晴天，则这一段时间有（ ）| A． | 9天 | B． | 11天 | C． | 13天 | D． | 22天 |
分析 解法一：根据题意设有x天早晨下雨，这一段时间有y天；有9天下雨，即早上下雨或晚上下雨都可称之为当天下雨，①总天数-早晨下雨=早晨晴天；②总天数-晚上下雨=晚上晴天；列方程组解出即可．
解法二：列三元一次方程组，解出即可．
解答 
解：解法一：设有x天早晨下雨，这一段时间有y天，
根据题意得：$\left\{\begin{array}{l}{y-x=7①}\\{y-（9-x）=6②}\end{array}\right.$
①+②得：2y=22
y=11
所以一共有11天，
解法二：设一共有x天，早晨下雨的有y天，晚上下雨的有z天，
根据题意得：$\left\{\begin{array}{l}{y+z=9}\\{x-z=6}\\{x-y=7}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=11}\\{y=4}\\{z=5}\end{array}\right.$，
所以一共有11天，
故选B．
点评 本题以天气为背景，考查了学生生活实际问题，恰当准确设未知数是本题的关键；根据生活实际可知，早晨和晚上要么下雨，要么晴天；本题也可以用算术方法求解：（9+6+7）÷2=11．
练习册系列答案
名校课堂系列答案
相关题目
2．方程x2+x-12=0的两个根为（ ）
| A． | x1=-2，x2=6 | B． | x1=-6，x2=2 | C． | x1=-3，x2=4 | D． | x1=-4，x2=3 |
19．与$\sqrt{2}$是同类二次根式的为（ ）
| A． | $\sqrt{8}$ | B． | $\sqrt{3}$ | C． | $\sqrt{12}$ | D． | $\sqrt{6}$ |
3．
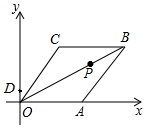已知菱形OABC在平面直角坐标系的位置如图所示，顶点A（5，0），OB=4$\sqrt{5}$，点P是对角线OB上的一个动点，D（0，1），当CP+DP最短时，点P的坐标为（ ）
已知菱形OABC在平面直角坐标系的位置如图所示，顶点A（5，0），OB=4$\sqrt{5}$，点P是对角线OB上的一个动点，D（0，1），当CP+DP最短时，点P的坐标为（ ）| A． | （0，0） | B． | （1，$\frac{1}{2}$） | C． | （$\frac{6}{5}$，$\frac{3}{5}$） | D． | （$\frac{10}{7}$，$\frac{5}{7}$） |
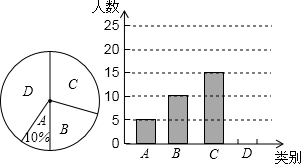
20．
秋季新学期开学时，红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试，测试成绩全部合格，现学校随机选取了部分学生的成绩，整理并制作成了如下不完整的图表：
请根据上述统计图表，解答下列问题：
（1）在表中，a=0.1，b=0.3，c=18；
（2）补全频数直方图；
（3）根据以上选取的数据，计算七年级学生的平均成绩．
（4）如果测试成绩不低于80分者为“优秀”等次，请你估计全校七年级的800名学生中，“优秀”等次的学生约有多少人？
秋季新学期开学时，红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试，测试成绩全部合格，现学校随机选取了部分学生的成绩，整理并制作成了如下不完整的图表：| 分 数 段 | 频数 | 频率 |
| 60≤x＜70 | 9 | a |
| 70≤x＜80 | 36 | 0.4 |
| 80≤x＜90 | 27 | b |
| 90≤x≤100 | c | 0.2 |
（1）在表中，a=0.1，b=0.3，c=18；
（2）补全频数直方图；
（3）根据以上选取的数据，计算七年级学生的平均成绩．
（4）如果测试成绩不低于80分者为“优秀”等次，请你估计全校七年级的800名学生中，“优秀”等次的学生约有多少人？
如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别是A（2，2），B（4，0），C（4，-4）