题目内容
1．若x2+mx+n分解因式的结果是（x+2）（x-1），则m+n的值为-1．分析 先把（x+2）（x-1）展开，求得m，n的值，再求m+n的值即可．
解答 解：∵x2+mx+n分解因式的结果是（x+2）（x-1），
∴x2+mx+n=x2+x-2，
∴m=1，n=-2，
∴m+n=1-2=-1，
故答案为-1．
点评 本题考查了因式分解-十字相乘法，求得m，n的值是解题的关键．
练习册系列答案
相关题目
11．下列分解因式正确的是（ ）
| A． | 2x2+4xy=x（2x+4y） | B． | 4a2-4ab+b2=（2a-b）2 | ||
| C． | x3-x=x（x2-1） | D． | 3x2-5xy+x=x（3x-5y） |
12．
如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于（1，0）及（x1，0），且-2＜x1＜-1，与y轴的交点在（0，2）上方，则下列结论中错误的是（ ）
如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于（1，0）及（x1，0），且-2＜x1＜-1，与y轴的交点在（0，2）上方，则下列结论中错误的是（ ）| A． | abc＞0 | B． | a+b+c=0 | C． | 2a-b＞-1 | D． | 2a+c＜0 |
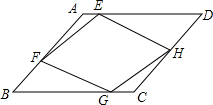菱形ABCD的边长为4，∠B=60°，F、H分别是AB、CD的中点，E、G分别在AD、BC上，且AE=CG．
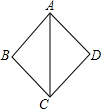如图，在△ABC和△ADC中，下列结论：
如图，Rt△ABC中，若∠ACB=90°，AC=4，BC=3，将△ABC绕着C点旋转，使得B点落在AB上的B′处，A点落在A′处，则AA′=$\frac{24}{5}$．