题目内容
12. 如图,在Rt△ABC中,∠ACB=90°,D为斜边的中点,点E、点F分别在直线CA、BC上,且DE⊥DF.
如图,在Rt△ABC中,∠ACB=90°,D为斜边的中点,点E、点F分别在直线CA、BC上,且DE⊥DF.(1)证明:△DEF是等腰直角三角形;
(2)求证:EF2=AE2+BF2;
(3)若AE=5,BF=12,求S△CEF的值;
(4)探索S△CEF、S△DEF、S△ABC之间的数量关系.
分析 (1)连接CD,根据等腰直角三角形的性质得到CD⊥AB,AD=DB=CD,∠A=∠B=∠ACD=∠DCB=45°,由余角的性质得到∠ADE=∠CDF,推出△ADE≌△CDF,根据全等三角形的性质得到DE=DF,于是得到结论;
(2)延长FD,使DM=DF,连接AM,EM,通过△DFB≌△AMD,得到AM=BF,∠B=∠DAM=45°,证得∠CAD+DAM=90°,根据勾股定理得到AE2+AM2=EM2,等量代换得到EF2=AE2+BF2;
(3)根据全等三角形的性质得到CF=AE=5,BC=17=AC,求得BF=CE=12,于是得到结论;
(4)根据三角形全等得到S△ADE=S△CDF,由S△ADE+S△CDE=$\frac{1}{2}$S△ABC=S△CDF+S△BDF,于是得到S△BDF=S△CDE,推出S△ADE+S△BDF=$\frac{1}{2}$S△ABC,即可得到结论.
解答 (1)证明:连接CD,
∵△ABC是等腰直角三角形,
∴CD⊥AB,AD=DB=CD,∠A=∠B=∠ACD=∠DCB=45°,
∵ED⊥DF,
∴∠CDE+∠CDF=90°,
∴∠ADE=∠CDF,
在△ADE与△CDF中,
$\left\{\begin{array}{l}{∠ADE=∠CDF}\\{AD=CD}\\{∠A=∠DCF}\end{array}\right.$,
∴△ADE≌△CDF,
∴DE=DF,
∴△DEF是等腰直角三角形;
(2)延长FD,使DM=DF,连接AM,EM, 在△DFB与△AMD中,
在△DFB与△AMD中,
$\left\{\begin{array}{l}{DM=DF}\\{∠ADM=BDF}\\{AD=DB}\end{array}\right.$,
∴△DFB≌△AMD,
∴AM=BF,∠B=∠DAM=45°,
∴∠CAD+DAM=90°,
∴AE2+AM2=EM2,
∵DE⊥DF,DM=DF,
∴EF=EM,
∴EF2=AE2+BF2;
(3)∵△AED≌△CDF,
∴CF=AE=5,
∴BC=17=AC,
∴BF=CE=12,
∴S△CEF=$\frac{1}{2}CE•CF$=$\frac{1}{2}×12×5$=30;
(4)∵△AED≌△CDF,
∴S△ADE=S△CDF,
∵S△ADE+S△CDE=$\frac{1}{2}$S△ABC=S△CDF+S△BDF,
∴S△BDF=S△CDE,
∴S△ADE+S△BDF=$\frac{1}{2}$S△ABC,
∴S△DEF+S△CEF=$\frac{1}{2}$S△ABC.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质和判定,线段垂直平分线的性质,正确的作出辅助线是解题的关键.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案 如图,下列语句正确的是( )
如图,下列语句正确的是( )| A. | 线段AB与线段BC是同一条线段 | B. | 直线AB与直线是BC同一条直线 | ||
| C. | 点A在线段BC上 | D. | 点C在射线BA上 |
| A. | $8\sqrt{3}-2\sqrt{3}=6$ | B. | $5\sqrt{3}+5\sqrt{2}=10\sqrt{5}$ | C. | $4\sqrt{3}×2\sqrt{2}=8\sqrt{6}$ | D. | $4\sqrt{2}÷2\sqrt{2}=2\sqrt{2}$ |
 如图,四边形ABCD内接于圆,AD=DC,点E在CD的延长线上.若∠ADE=80°,则∠ABD的度数是40°.
如图,四边形ABCD内接于圆,AD=DC,点E在CD的延长线上.若∠ADE=80°,则∠ABD的度数是40°.
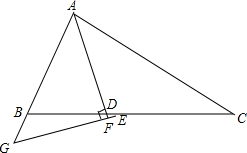 已知:△ABC中,∠ABC=2∠ACB,AD是∠BAC的角平分线,E是BC的中点,过E作EF⊥AD交AD的延长线于F,交AB的延长线于G,求证:BD=2BG.
已知:△ABC中,∠ABC=2∠ACB,AD是∠BAC的角平分线,E是BC的中点,过E作EF⊥AD交AD的延长线于F,交AB的延长线于G,求证:BD=2BG.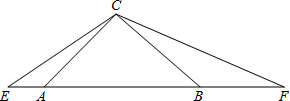 如图,在等腰三角形ABC中,∠ACB=90°,分别延长BA至点E,AB至点F,使得AE=2,且∠ECF=135°,若设AB=x,BF=y,试求出y与x之间的两数关系式.
如图,在等腰三角形ABC中,∠ACB=90°,分别延长BA至点E,AB至点F,使得AE=2,且∠ECF=135°,若设AB=x,BF=y,试求出y与x之间的两数关系式.