Question

4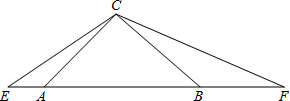．如图，在等腰三角形ABC中，∠ACB=90°，分别延长BA至点E，AB至点F，使得AE=2，且∠ECF=135°，若设AB=x，BF=y，试求出y与x之间的两数关系式．

Answer 1

分析 根据等腰直角三角形性质求出∠CAE=∠CBF=135°，求出∠ECA+∠BCF=45°，∠E+∠ACE=45°，推出∠E=∠BCF，即可推出两三角形相似；根据等腰直角三角形性质和锐角三角函数定义求出AC和BC长，根据相似得出比例式，代入即可求出答案．

解答 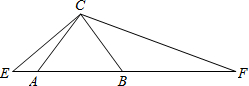证明：∵△ABC为等腰直角三角形，∠ACB=90°，
∴AC=BC，
∴∠CAB=∠CBA=45°，
∴∠CAE=180°-45°=135°，
同理∠CBF=135°，
∴∠CAE=∠CBF，
∵∠ECF=135°，∠ACB=90°，
∴∠ECA+∠BCF=45°，
∵∠ECA+∠E=∠CAB=45°，
∴∠E=∠BCF，
∵∠CAE=∠CBF，
∴△ECA∽△CFB；
∵AB=x，∠CAB=45°，∠ACB=90°，AC=BC，
∴sin45°=$\frac{CB}{x}$，
∴CB=$\frac{\sqrt{2}}{2}$x=AC，
∵由（1）知△ECA∽△CFB，
∴$\frac{AE}{CB}$=$\frac{AC}{BF}$，
∴$\frac{2}{\frac{\sqrt{2}}{2}x}$=$\frac{\frac{\sqrt{2}}{2}x}{y}$，
∴y=$\frac{1}{4}$x²，
即y与x之间的函数关系式是y=$\frac{1}{4}$x²．

点评 本题考查了相似三角形的性质和判定，等腰直角三角形性质，锐角三角函数的定义等知识点，通过做此题培养了学生的分析问题和解决问题的能力．