题目内容
10．
如图，四边形ABCD内接于圆，AD=DC，点E在CD的延长线上．若∠ADE=80°，则∠ABD的度数是40°．
分析 根据弦、弧、圆心角的关系得到$\widehat{AD}$=$\widehat{DC}$，根据圆周角定理得到∠ABD=∠CBD，根据圆内接四边形的性质得到∠ABC=80°，得到答案．
解答 解：∵AD=DC，
∴$\widehat{AD}$=$\widehat{DC}$，
∴∠ABD=∠CBD，
∵∠ADE=80°，
∴∠ABC=80°，
∴∠ABD=$\frac{1}{2}$∠ABC=40°，
故答案为：40°．
点评 本题考查的是圆内接四边形的性质和弦、弧、圆心角的关系，掌握圆内接四边形的任意一个外角等于它的内对角是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
20．已知x=1是方程2x2-3x-m=0的一个根，则m的值为（ ）
| A． | 1 | B． | 5 | C． | -1 | D． | -5 |
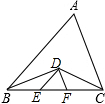如图所示，在△ABC中，BD、CD分别是∠ABC、∠ACB的平分线，DE∥AB，DF∥AC，若△DEF的周长为100cm，则BC的长为100cm．
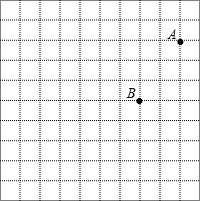如图是由边长为1的小正方形组成的方格图．
15．
如图，在边长为1的正方形网格中，△ABC的三边a，b，c的大小关系是（ ）
如图，在边长为1的正方形网格中，△ABC的三边a，b，c的大小关系是（ ）| A． | c＜b＜a | B． | c＜a＜b | C． | a＜c＜b | D． | a＜b＜c |
如图，在Rt△ABC中，∠ACB=90°，D为斜边的中点，点E、点F分别在直线CA、BC上，且DE⊥DF．