题目内容
14.用a,b,c作三角形的三边,其中不能构成直角三角形的是( )| A. | a=$\sqrt{1}$,b=$\sqrt{2}$,c=$\sqrt{3}$ | B. | a=2,b=3,c=4 | C. | a=12,b=5,c=13 | D. | a=$\sqrt{7}$,b=2,c=$\sqrt{3}$ |
分析 根据勾股定理的逆定理计算,判断即可.
解答 解:($\sqrt{1}$)2+($\sqrt{2}$)2=($\sqrt{3}$)2,
则A能构成直角三角形;
22+32≠42,
则B不能构成直角三角形;
122+52=132,
则C能构成直角三角形;
22+($\sqrt{3}$)2=($\sqrt{7}$)2,
则D能构成直角三角形;
故选:B.
点评 本题考查的是勾股定理的逆定理的应用,勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
17. 如图,在等腰直角三角形ABC中,直角边AB=AC=4,以AB为直径的半圆交斜边BC于点D,则图中阴影部分的面积为(结果保留π)( )
如图,在等腰直角三角形ABC中,直角边AB=AC=4,以AB为直径的半圆交斜边BC于点D,则图中阴影部分的面积为(结果保留π)( )
 如图,在等腰直角三角形ABC中,直角边AB=AC=4,以AB为直径的半圆交斜边BC于点D,则图中阴影部分的面积为(结果保留π)( )
如图,在等腰直角三角形ABC中,直角边AB=AC=4,以AB为直径的半圆交斜边BC于点D,则图中阴影部分的面积为(结果保留π)( )| A. | 6-π | B. | 8-π | C. | 8-2π | D. | 4 |
 已知等腰三角形的周长为6cm,底边长y(cm)是腰长x(cm)的函数,
已知等腰三角形的周长为6cm,底边长y(cm)是腰长x(cm)的函数,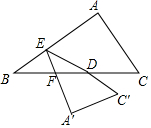 在Rt△ABC中,AC=3,AB=4,D为斜边BC中点,E为AB上一个动点,将△ABC沿直线DE折叠,A、C的对应点分别为A′、C′,EA′交BC于点F,若△BEF为直角三角形,则BE的长度为$\frac{1}{2}$或$\frac{5}{4}$.
在Rt△ABC中,AC=3,AB=4,D为斜边BC中点,E为AB上一个动点,将△ABC沿直线DE折叠,A、C的对应点分别为A′、C′,EA′交BC于点F,若△BEF为直角三角形,则BE的长度为$\frac{1}{2}$或$\frac{5}{4}$.